В прямоугольной трапеции боковые стороны равны 15см и 9см, а большее основание-17см. Найдите площадь трапеции.
Приложения:
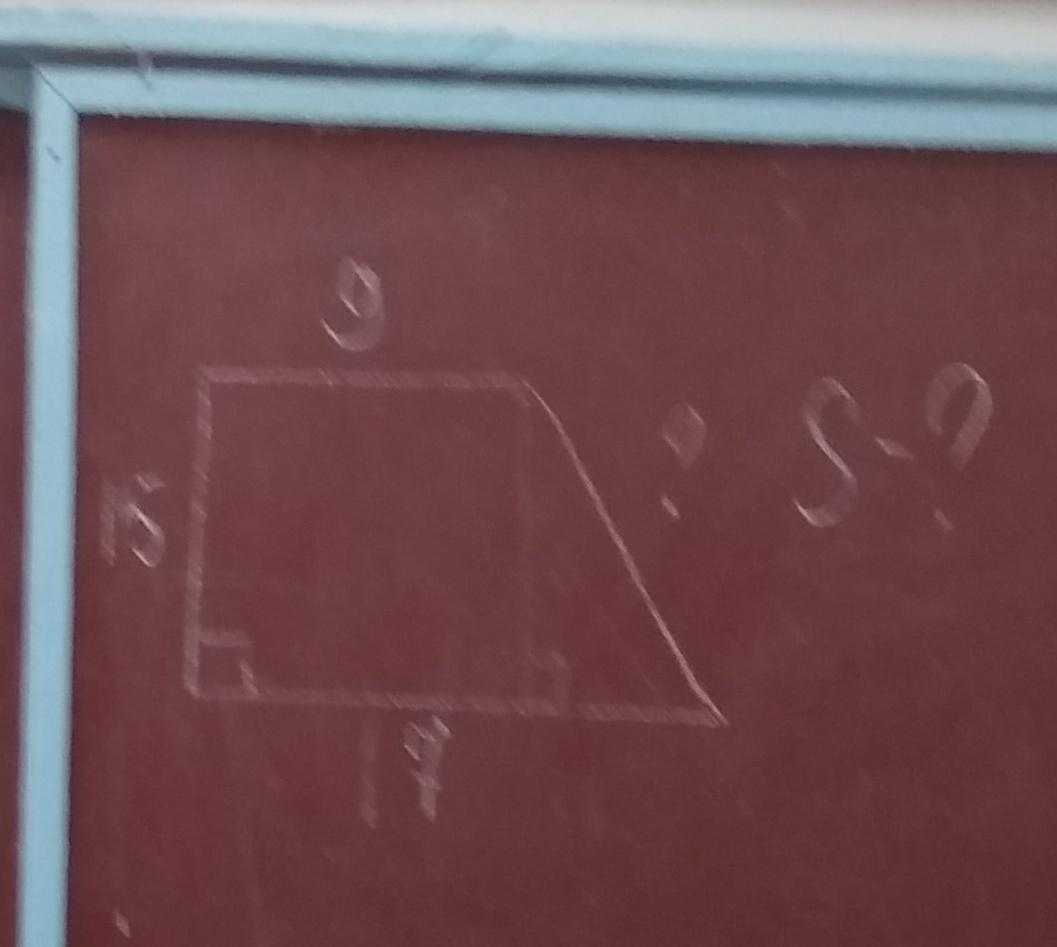
Ответы
Ответ дал:
0
Ответ:
99 см²
Объяснение:
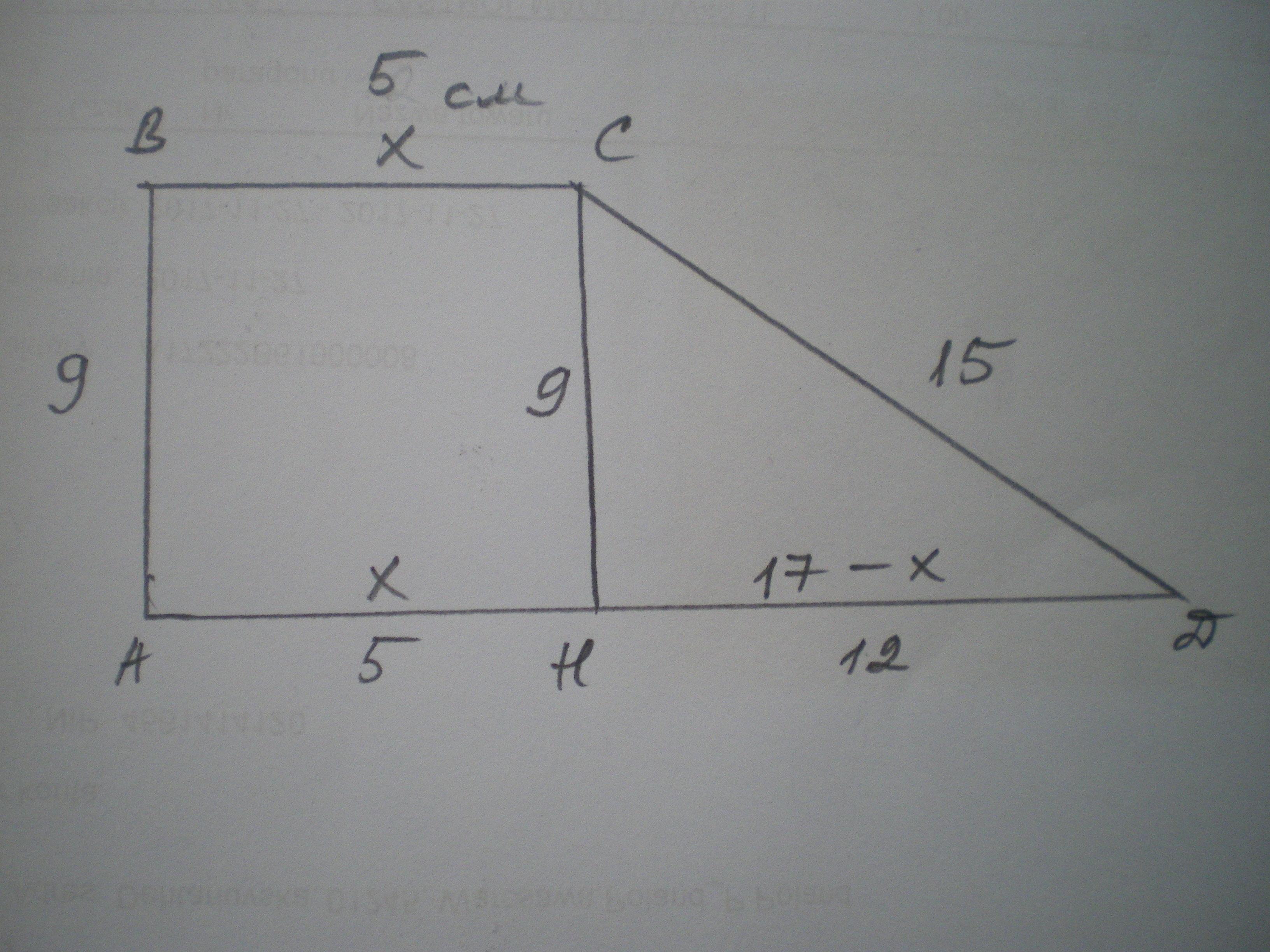
Дано: АВСД - трапеция, ∠А=∠В=90°, АВ=9 см, СД=15 см. АД=17 см. Найти S(АВСД)
Пусть ВС = х см. Проведем высоту СН=АВ=9 см. Тогда АН=ВС=х см, ДН=17-х см.
Рассмотрим ΔСДН - прямоугольный.
ДН²=(ДС²-СН²)
(17-х)²=225-81
289-34х+х²=144
х²-34х+145=0
х=29 (не подходит по условию)
х=5.
ДН=17-5=12 см.; ВС=5 см.
S=(ВС+АД):2*СН=(5+17):2*9=99 см²
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад