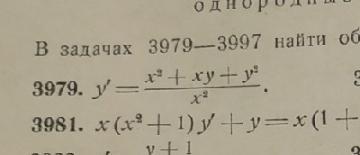Question

Помогите решит дифференциальное уравнение. номер 3979

Answer 1

Пошаговое объяснение:

Данное дифференциальное уравнение является однородным.

Пусть y = ux, тогда y' = u'x + u.

$u'x+u=dfrac{x^2+ux^2+u^2x^2}{x^2}\ \ u'x+u=1+u+u^2\ \ u'x=1+u^2$

Получили уравнение с разделяющимися переменными

$dfrac{du}{dx}=dfrac{1+u^2}{x}~~~Longleftrightarrow~~~ displaystyle intdfrac{du}{1+u^2}=intdfrac{dx}{x}\ \ \ {rm arctg}, u=ln |x|+C\ u={rm tg}, left(ln |x|+Cright)~~~~Longrightarrow~~~~ boxed{y=x{rm tg}left(ln |x|+Cright)}$