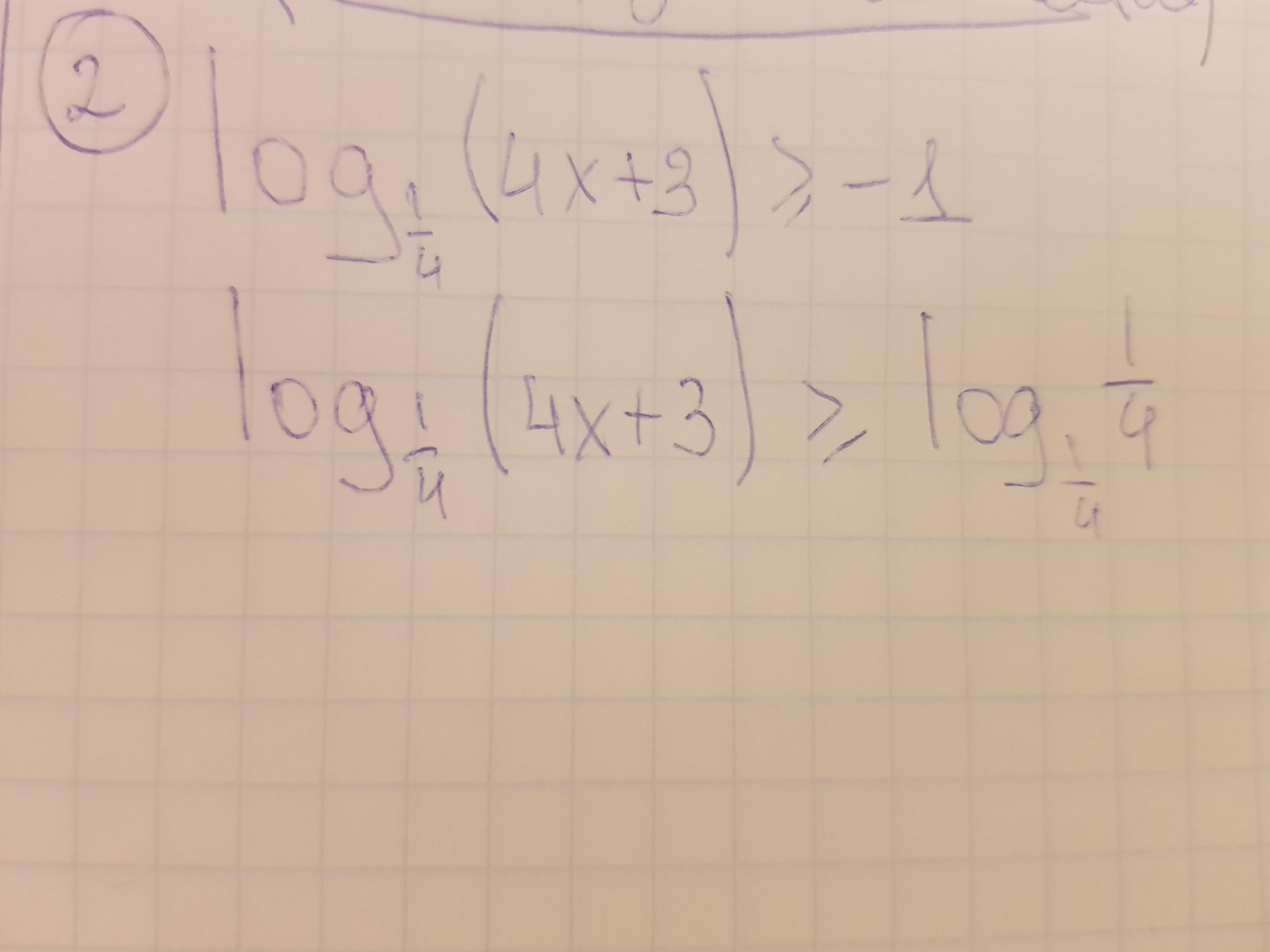Ответы
Ответ дал:
0
ОДЗ :
4x + 3 > 0
4x > - 3
x >-0,75
x ∈ (- 0,75 ; + ∞)
x ∈ (- ∞ ; 0,25]
С учётом ОДЗ окончательный ответ : x ∈ (- 0,75 ; 0,25]
Ответ дал:
0
-1= log(1/4) 4
Ответ дал:
0
Использую метод рационализации:
но, с учётом ОДЗ:
Ответ:
Вас заинтересует
3 года назад
3 года назад
9 лет назад
10 лет назад