Question

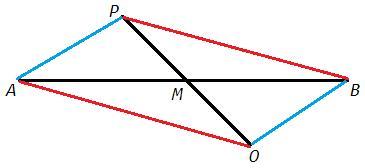
Отрезки AB и PO пересекаются в точке М, причем точка М является серединой каждого из
этих отрезков. Докажите, что AP + BP = AO +ВО.
​

Answer 1

Диагонали четырехугольника APBO точкой пересечения делятся пополам. Следовательно APBO - параллелограмм (по признаку), его противоположные стороны равны.

AP=BO, BP=AO => AP+BP =AO+BO

Answer 2

а можете ещё если не трудно :)

Answer 3

внизу смотрите на мои вопросы

Answer 4

4 и 5 задания

Answer 5

ДОКАЗАТЕЛЬСТВО:

Диагонали четырехугольника APBO точкой пересечения делятся пополам.

Следовательно, АРВО — параллелограмм.

AP = BO;

BP = AO;

отсюда следует: AP + BP = AO + BO

~•~•~•ZLOY_TIGROVSKIY~•~•~•

Answer 6

полответа с**зжено из предыдущего ответа

Answer 7

Что?