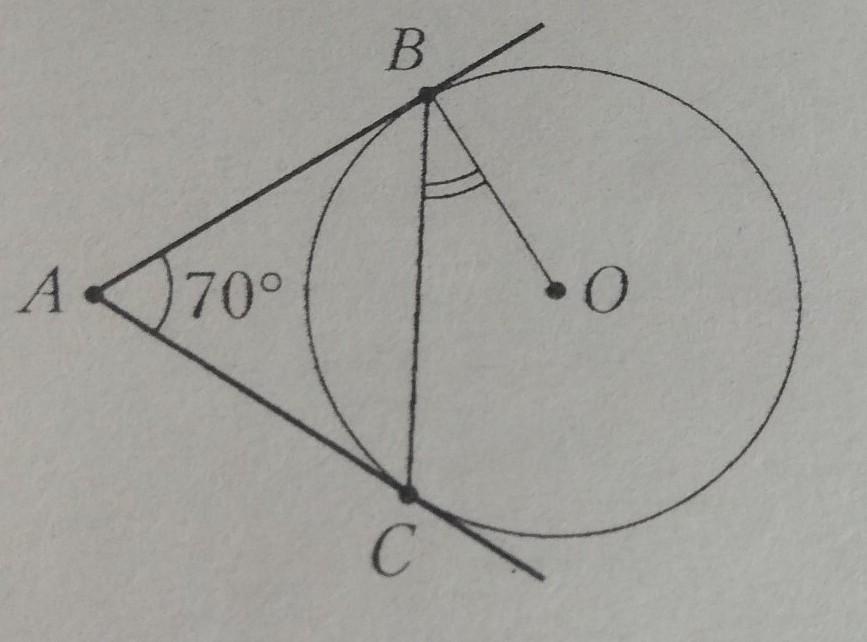
Лучи AB и AC касаются окруж-
ности с центром о в точках
В и С, угол BAC = 70°.
Найдите угол ОВС.
70°
Приложения:
Ответы
Ответ дал:
0
Ответ:
Объяснение:
Проведём ещё один радиус ОС и отрезок АО.По свойствам 2 касательных, проведённых из одной точки образовались 2 равных треугольника ΔАСО=ΔАВО(АО-общая сторона,АВ=АС ,как отрезки касательных к окружности, проведенных из одной точки,ОС=ОВ как радиусы ).Угол СОА=180°-уг.С-уг.САО=180°-90°-35°=55°
Значит уг.СОВ=2*угол СОА=55°*2=110°
ΔСОВ-равнобедренный,углы при основе равны.
угол ОВС=(180°-уг.СОВ):2=(180°-110°):2=70°:2=35°
Вас заинтересует
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад