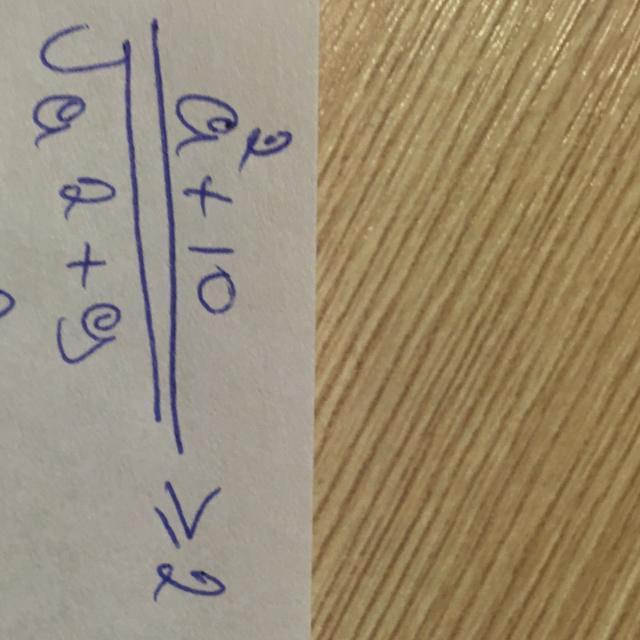
Ответы
Ответ дал:
0
давай попробуем вот так
Может так
6V(y^2+3)/(y^2+12)<=1 умножим все на y^2+12
6*V(y^2+3)<=y^2+12 возведем в квадрат
36*(y^2+3)<=y^4+24y^2+144
36y^2+108-y^4-24y^2-144<=0
-y^4+12y^2-36<=0 умножим на (-1)
y^4-12y^2+36>=0
y^2=x
x^2-12x+36=0
D=(-12)^2-4*1*36=0
x=(-(-12))/2=6
(x-6)^2>=0
(y^2-6)^2>=0
при любых значениях у, квадрат будет больше или равен 0.
Ответ дал:
0
попробуй по этому примеру может получиться
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
10 лет назад
10 лет назад