Помагите решить задачу!
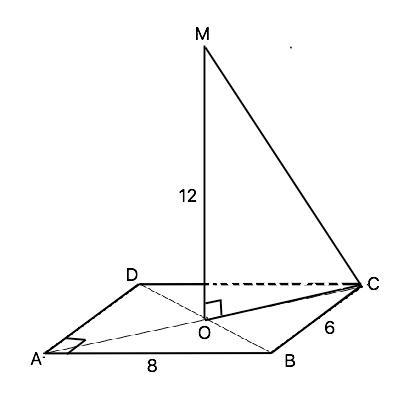
ABCD прямоугольник. MO перпендикулярен ABC, MO=12, АВ=6, AD=8. Найдите MC.
Ответы
Ответ дал:
0
Ответ: 13 (ед. длины)
Объяснение: О - точка пересечения диагоналей прямоугольника. Т.к. МО⊥АВС, , а АВС принадлежит плоскости АВСD, МО⊥АВСD. Нужный отрезок МС найдём из прямоугольного ∆ МОС.
ОС - половина диагонали прямоугольника. ОС=0,5•АС=0,5•√(AB²+BC²)=0,5√(8²+6²)=5 ⇒
МС=√(MO²+OC²)=√(12²+5²)=13 (ед. длины).
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад