Question

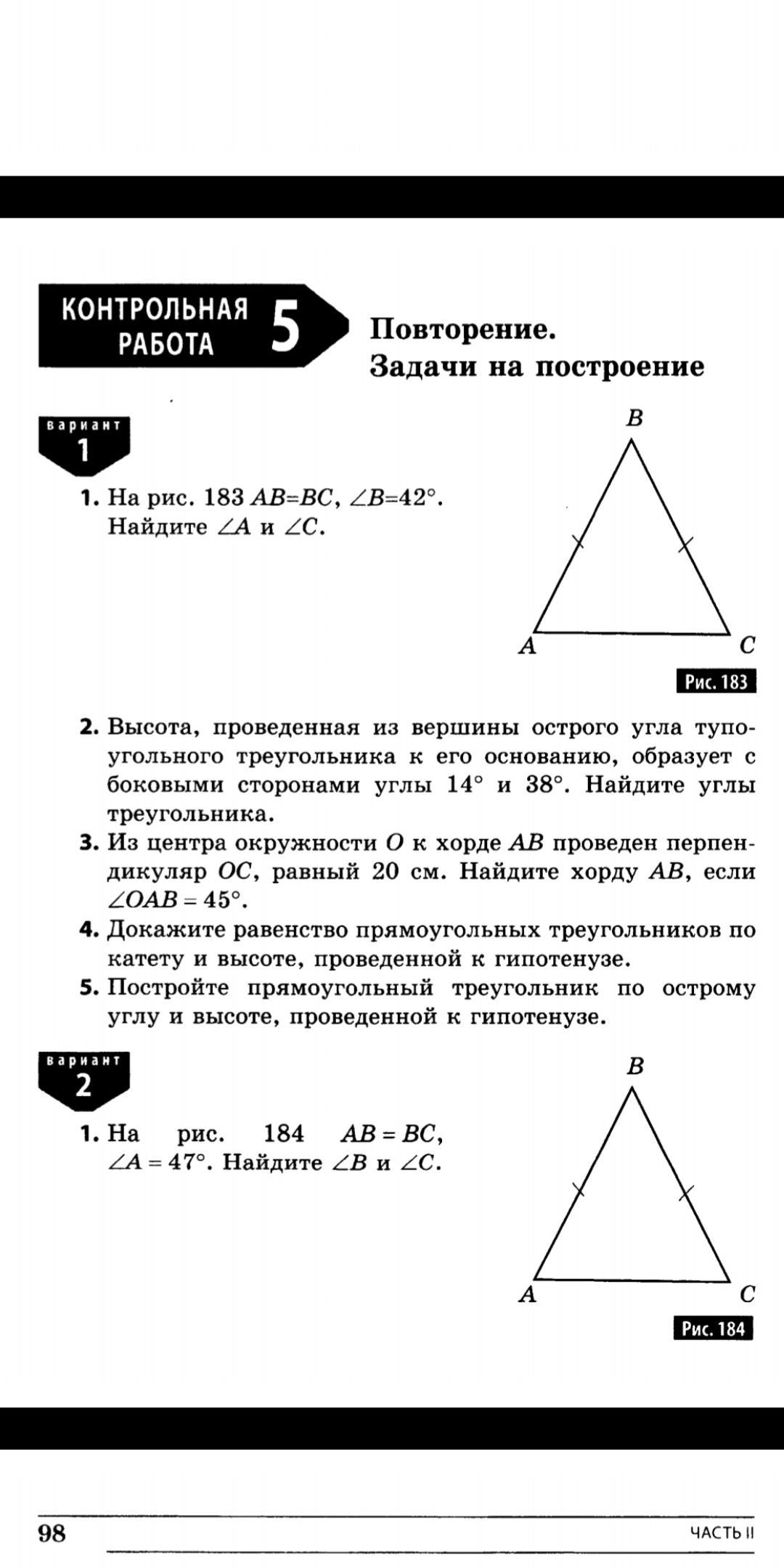
1. На рис. 183 AB=BC, ZB=42°


Найдите ZA и 2С.


Рис. 183


2. Высота, проведенная из вершины острого угла тупо- угольного треугольника к его основанию, образует с боковыми сторонами углы 14° и 38°. Найдите углы треугольника.


3. Из центра окружности О к хорде АВ проведен перпен- дикуляр ОС, равный 20 см. Найдите хорду АВ, если ZOAB = 45°.


4. Докажите равенство прямоугольных треугольников по


катету и высоте, проведенной к гипотенузе.


5. Постройте прямоугольный треугольник по острому


углу и высоте, проведенной к гипотенузе.

Answer 1

Ответ:

Объяснение:

номер 1

1) Так как углы при основании равны, а это углы А и В, получается, что угол А + угол В = 180 - 42 = 138, а 138/2=69 градусов равны углы А и В

номер 2

1) У нас получается прямоугольный треугольник с прямым углом и углом в 14°,а по теореме о сумме углов треугольника  ∠3=180°-90°-14°=76°

номер 3

1)∠АОС=∠ОАС как односторонние углы равны в р/б ∡ с основанием АО=>ОС=АС=20 см, как боковые стороны.

2)Проведем отрезок ОВ.

3)Рассмотрим треугольники АОС и ОВС:

1. АО=ОВ как радиусы
2. ОС-общая

и из этого следует, что ∡АОС=∡ОВС=>АС+СИ=20 см

3)20 см+20 см=40 см

номер 4

Они будут равны по стороне и двум прилежащим к ней углам

Answer 2

Ответ:

1-69

Объяснение:

180-42=138 градусов

138:2=69 градусов