Question

СРОЧНО 40 БАЛОВ

Стороны параллелограмма равны 6см и 7см, угол между ними 60 градусов . Найти высоты параллелограмма.

Answer 1

${6}^{2} = {x}^{2} + {3}^{2} \ 36 = {x}^{2} + 9 \ {x}^{2} = 27 \ x = sqrt{27 } = 3 sqrt{3}$

Answer 2

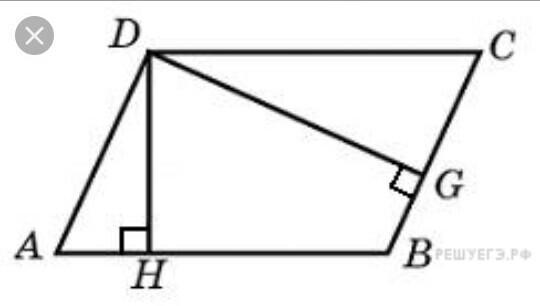
Дано: АД=6 см, АВ=7 см, уголА=60 градусов.

Найти: ДН, ДG.

Решение:

BC=AD=6 см.

Рассм. треуг. АДН: угол АНД=90 градусов, АД=6 см, уголА=60 градусов. По sinА найдем ДН:

$frac{ sqrt{3} }{2} = frac{ x}{6} \ x = frac{6 sqrt{3} }{2} \ x = 3 sqrt{3}$

Sabcd=AB×DH=BC×DG.

$s = 3 sqrt{3} times 7 = 21 sqrt{3}$

DG=S/BC.

$frac{21 sqrt{3} }{6} = 3.5 sqrt{3}$

Ответ:

$3.5 sqrt{3}$ см, 3√3 см.

Answer 3

Спасибо!