У некоторой геометрической прогрессии сумма членов на нечётных местах равна 21/16,а сумма членов на чётных местах равна 21/32.Найти знаменатель этой прогрессии,если число членов прогрессии чётное.
Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
Приложения:
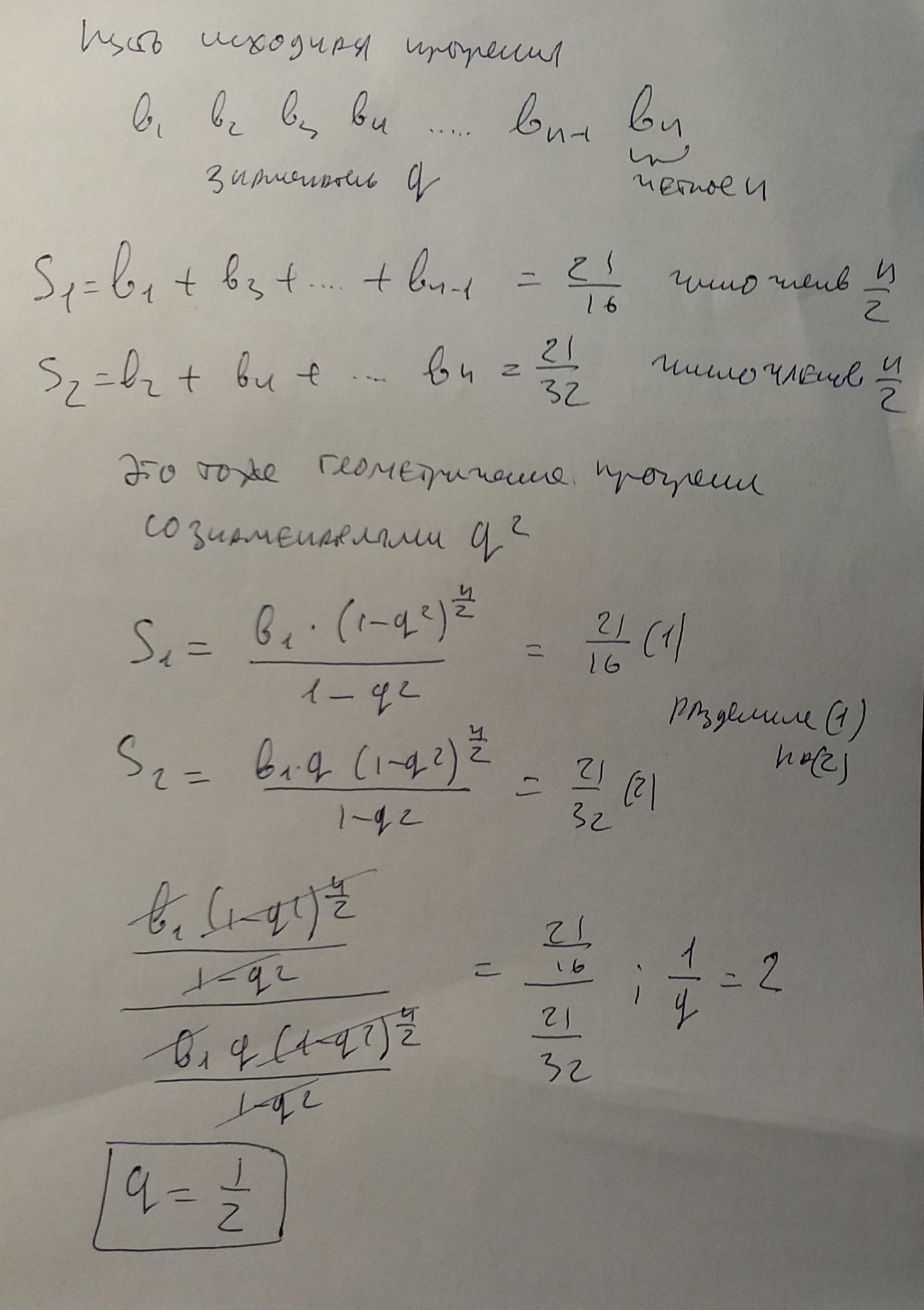
Ответ дал:
0
Докажем, что в конечной геометрической прогрессии, имеющей четное число членов, отношение суммы членов, стоящих на четных местах, к сумме членов, стоящих на нечетных местах, равно знаменателю прогрессии. А именно, 21/32:(21/16)=21/32*16/21=1/2
Распишем отношение суммы членов, стоящих на четных местах, к сумме членов, стоящих на нечетных местах,
(в₂+в₄+в₆+...в₂ₙ)/(в₁+в₃+в₅+...в₂ₙ-₁)=q*(в₁+в₃+в₅+...в₂ₙ-₁)/(в₁+в₃+в₅+...в₂ₙ-₁)=q
Ответ 1/2
Приложения:
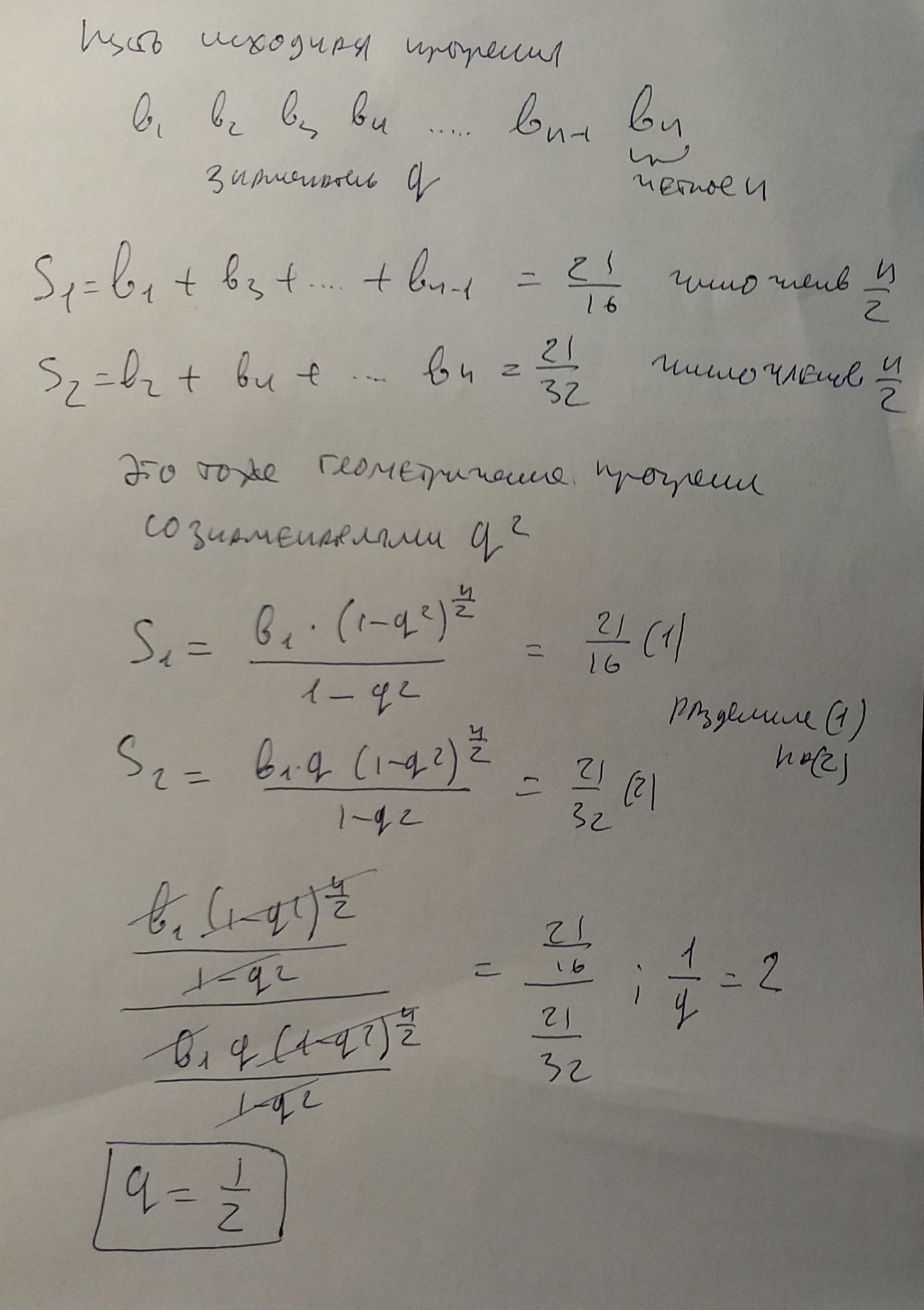
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад