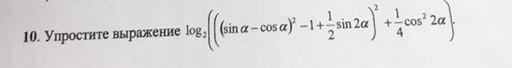Question

упростите выражение, срочно, завтра кр​

Answer 1

$log_{2}(((Sinalpha-Cosalpha)^{2}-1+frac{1}{2}Sin2alpha)^{2}+frac{1}{4}Cos^{2}2alpha)=log_{2} ((Sin^{2}alpha-2Sinalpha Cosalpha+Cos^{2}alpha-1+frac{1}{2}Sin2alpha)^{2}+frac{1}{4}Cos^{2}2alpha)=log_{2}((1-Sin2alpha-1+frac{1}{2}Sin2alpha)^{2} +frac{1}{4} Cos^{2}2alpha)=log_{2} ((-frac{1}{2}Sin2alpha)^{2}+frac{1}{4}Cos^{2}2alpha)=log_{2}(frac{1}{4}Sin^{2}2alpha+frac{1}{4}Cos^{2}2alpha)=log_{2}frac{1}{4}=-2$

Answer 2

эммм, решение можно?

Answer 3

А то ,что я написала, что по- вашему, если не решение ?

Answer 4

прости пожалуйста, спасибо большое, очень благодарен

Answer 5

sin (2x) = 2sin(x)cos(x)

sin² (x) + cos² (x) = 1

log(a) b = c     a^c = b

=========================

(sin(x) - cos(x) )² - 1 + 1/2*sin(2x) = sin² (x) - 2sin(x)cos(x) + cos²(x) - 1 + 1/2*sin(2x) = 1 - sin(2x)+1/2*sin(2x) - 1 = - 1/2*sin(2x)

(-1/2*sin(2x))² = 1/4*sin²(2x)

log(2) (1/4*sin²(2x) + 1/4*cos²(2x)) = log(2) 1/4*(sin²(2x) + cos²(2x)) = log(2) 1/4 = log(2) 2⁻² = -2

Answer 6

напиши сбер