Question

помогите плз !!!!!!!!!!!!!!!!!!!!!!

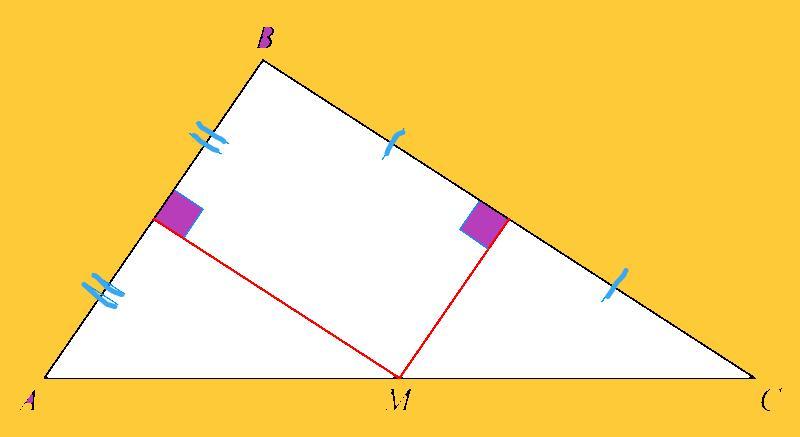
Серединные перпендикуляры к сторонам AB и BC треугольника ABC пересекаются в точке M, которая принадлежит стороне AC. Докажите, что точка M — середина отрезка AC.

Answer 1

Рассмотрим прямоугольник HBKM (допустим).

ВК = НМ; НВ=КМ

Рассмотрим треугольник АНМ и  МКС

МК=НВ, а АН=НВ (по условию), тогда МК=АН

ВК = НМ, а КС=ВК (по условию), тогда КС=НМ

углы АНМ=МКС, следовательно треугольники равны, значит все их элементы также равны. От суда следует, что гипотенузы АМ и МС равны, значит точка М — середина отрезка AC, что и требовалось доказать

Answer 2

Благодарю за решение

Answer 3

Точка М (пересечение серединных перпендикуляров) является центром окружности описанной вокруг данного треугольника. Следовательно АМ и МС радиусы и они равны.