СРОЧНО ПОМОГИТЕ ПОЖАЛУЙСТА
объясните как из первого уравнения получилось второе
буду рада любому объяснению
Приложения:

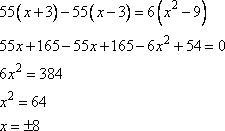
Ответы
Ответ дал:
0
Приводим левую часть к общему знаменателю.
Можем заметить в знаменателе формулу разности квадратов.
Решаем крест-накрест:
Ответ дал:
0
Левую часть домножили на x^2-9 и правую часть
Ответ дал:
0
Крест-накрест - это 6 мы умножили на знаменатель, а 1 на числитель
Ответ дал:
0
Как в пропорциях
Ответ дал:
0
понятно
Ответ дал:
0
спасибо
Ответ дал:
0
Уравнение было приведено под общий знаменатель. Он будет: (х-3)(х+3)
А значит:
55 (от первой дроби уравнения) умножаем на (х+3).
Получаем 55(х+3)
55 (от второй дроби уравнения) умножаем на (х-3)
Получаем 55(х-3)
6 умножаем на (х-3)(х+3). Собрав в формулу получим х² - 9
Получаем 6(х² - 9)
Отбрасываем знаменатели, при этом указывая область допустимых значений, следующим образом:
ОДЗ:
х-3≠0
х+3≠0
_________
х≠3
х≠-3
_________
Вроде бы объяснил.
Ответ дал:
0
Область Допустимых значений, при которых выражение имеет смысл
Ответ дал:
0
ааа понятно
Ответ дал:
0
В таких простых уравнениях не стоит заморачиваться
Ответ дал:
0
В любых уравнениях очень даже стоит заморачиваться.
Ответ дал:
0
Это не неравенство, чтобы учитывать все ограничения. Существует много методов решения уравнений. В данном уравнении это лишнее для 7 класса.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад