Ответы
Ответ дал:
0
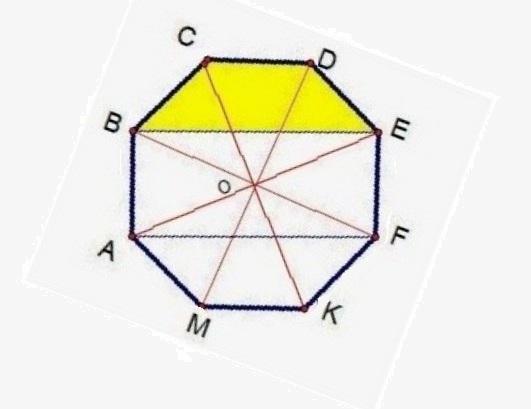
Проведем биссектрисы углов восьмиугольника, они пересекутся в точке О. Площадь восьмиугольника: (ABCDEFKM) =8* S (OEF).
Четырехугольник ABEF - параллелограмм (АВ//EF и АВ=EF). Диагонали параллелограмма равны: AE=BF (как диаметры описанной около восьмиугольника окружности), следовательно, ABEF - прямоугольник. Диагонали прямоугольника делят его на четыре равновеликих треугольника.
Площадь четырехугольника AFKM:
S (ABEF)= 4* S (OEF).
2*S (AFKM)=S (ABCDEFKM) - S (ABEF) =8* S (OEF)-4* S (OEF)=4* S (OEF).
S (AFKM)=2* S (OEF).
Теперь находишь отношение площади восьмиугольника к площади закрашенной части:
S (ABCDEFKM) : S (AFKM) = 8* S (OEF) : (2* S (OEF))=4.
Приложения:
Вас заинтересует
2 года назад
3 года назад
8 лет назад
9 лет назад