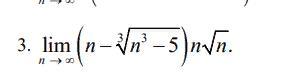Question

Вычислить предел функции, используя умножение на сопряженное выражение

Answer 1

Ответ:

Объяснение:

$limlimits_{n to infty}left(n-sqrt[3]{n^3-5} right)nsqrt{n}=limlimits_{n to infty}frac{left(n-sqrt[3]{n^3-5} right)(n^2+nsqrt[3]{n^3-5}+sqrt[3]{(n^3-5)^2})cdot nsqrt{n}}{n^2+nsqrt[3]{n^3-5}+sqrt[3]{(n^3-5)^2}} =\=limlimits_{n to infty}frac{left[n^3-left(n^3-5right)right]cdot nsqrt{n}}{n^2+nsqrt[3]{n^3-5}+sqrt[3]{(n^3-5)^2}}=limlimits_{n to infty}=5limlimits_{n to infty}frac{n^{frac{3}{2}}}{n^2+nsqrt[3]{n^3-5}+sqrt[3]{(n^3-5)^2}} = 0$

Старшая степень числителя равна 3/2, а старшая степень знаменателя равна 2. Следовательно, при стремлении n к бесконечности, знаменатель растёт быстрее числителя и предел равен 0.