Question

Нужна помощь в решении задачи!

Докажите, что если в тетраэдре два противоположных ребра перпендикулярны, то тетраэдр можно пересечь плоскостью так, что в сечении получится прямоугольник.

Answer 1

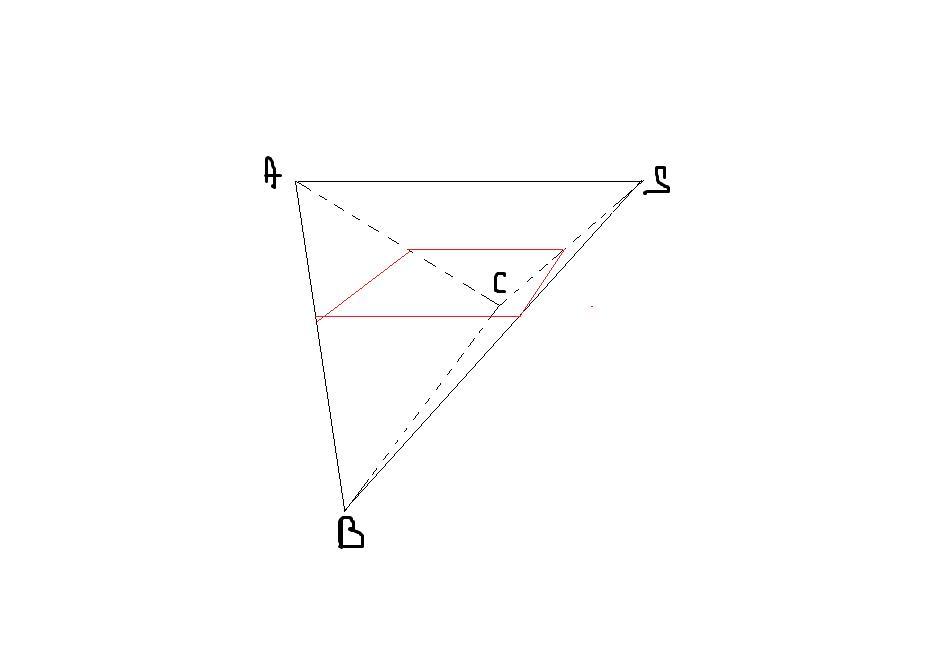
Докажем это предъявив построение такого сечения. Рассмотрим тетраэдр SABC. Сечение проведем так как показано на рисунке: стороны четырехугольника параллельны соответствующим ребрам в гранях, в которых эти стороны находятся. По условию SA перпендикулярно BC,  а значит соответствующий стороны четырехугольника также перпендикулярны. Аналогично и для оставшихся пар сторон. Итак, все углы четырехугольника равны 90 градусов, а, значит, он является прямоугольником