Question

у=х^2-1 и у=х+1 найти площадь фигуры ограниченной линиями ​

Answer 1

Ответ:

Вот пошаговое объяснение

Пошаговое объяснение:

Answer 2

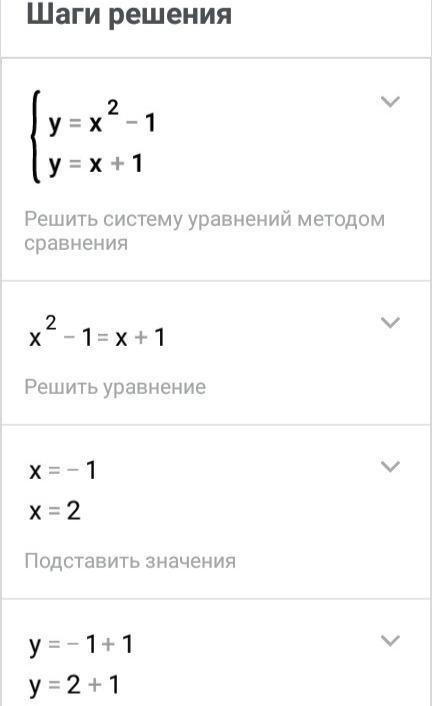
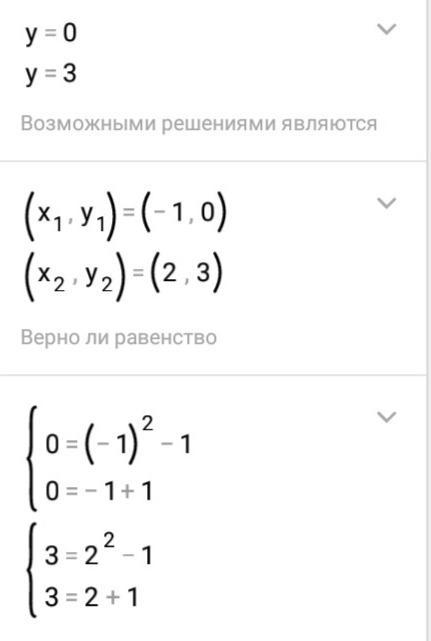
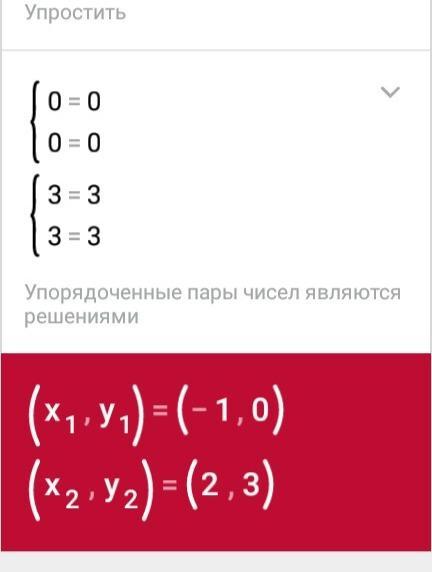
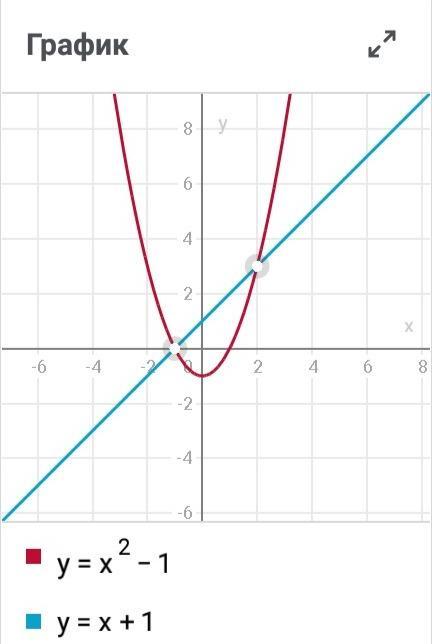
Найдем точки пересечения прямой у=х+1 и параболы у=х²-1

х²-1=х+1; х²-х-2=0; по  теореме, обратной теореме Виета, х₁=2; х₂=-1-это пределы интегрирования.

Найдем теперь площадь, отыскав определенный интеграл от минус единицы  до двух от функции (х+1-х²+1)дх=в пределах от минус один до двух ∫(х-х²+2)дх= х²/2-х³/3+2х

Вычислен по формуле Ньютона - Лейбница. От верхнего предела отнимем нижний. Получим    2 -8/3+4-1/2+1/3+2=5 целых 1/6/ед. кв./

Answer 3

https://znanija.com/task/32541513

Answer 4

помогите пожалуйста с дано и решением

Answer 5

все задание пождалуйста

Answer 6

мне к часу в школуууууууууууууу

Answer 7

Я решил. Но там условие - рисунок. Такой возможностью не обладаю. Разве сложно построить треугольник, в котором прямой угол?