Ответы
Ответ дал:
0
Ответ:
Объяснение:
Умножаем обе части на 2
Используем формулу:
https://ru-static.z-dn.net/files/d2e/eab21d54911a5ef9afe4a113c36b6dc1.png
Приложения:
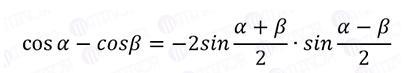
Ответ дал:
0
Приложения:
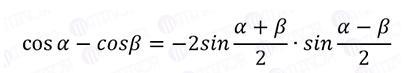
Вас заинтересует
3 года назад
3 года назад
9 лет назад