Question

куча баллов! ТОлько можно пожалуйста с рисунком и с дано

Боковые ребра треугольной пирамиды взаимно перпендикулярны, а их длины равны a. Найдите косинус угла, образованного плоскостью боковой грани с плоскостью основания.

Answer 1

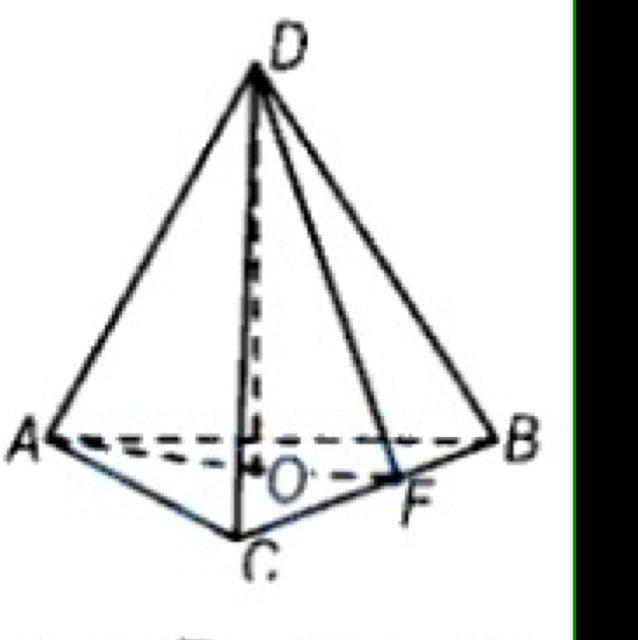
AF=AC sin60=а под корнем 6/2

OF=1/3AF=a под корнем 6/6

Угол CDF=45градусов значит

DF=CF =a под корнем2/2

OF/DF=под корнем 3/3

Answer 2

Это неправильное решение.

Answer 3

ок, а как?

Answer 4

у меня было 2 варианта либо 1/корень из 3, либо корень из3/3

Answer 5

Вернее неполное.

Answer 6

Неправильно???

Answer 7

Ответ:

Объяснение:

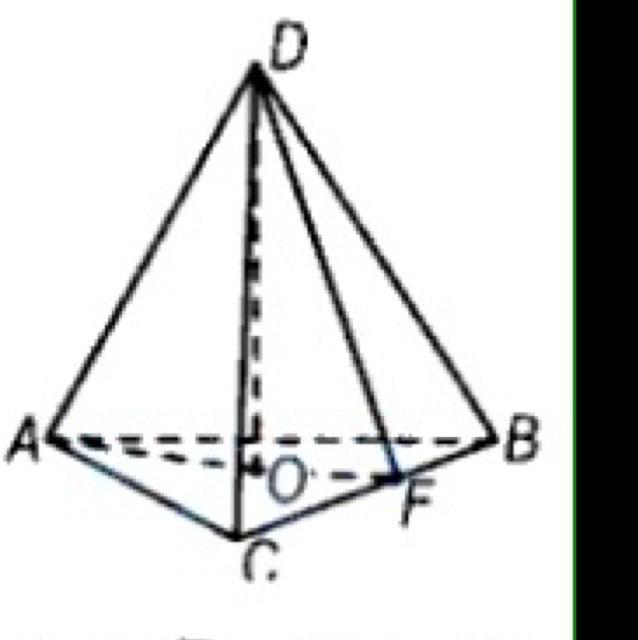
Так как боковые ребра пирамиды равны и углы между ними равны, то боковые грани тоже равны, значит ΔАВС правильный.

В прямоугольном тр-ке ВСД ДФ - высота и медиана, значит ВФ=СФ=ДФ.

ВС=СД√2=а√2 ⇒ ДФ=а√2/2.

Т.к. пирамида правильная, то высота, опущенная на основание, попадает в центр описанной и вписанной окружностей в самого основания.

ОФ=ВС√3/6=а√6/6.

В прямоугольном тр-ке ДОФ cosФ=ОФ/ДФ=(а/√6):(а/√2)=1/√3 - это ответ.