Question

Дана сфера и её касательная плоскость.
В плоскости находится точка; через неё и центр сферы проведена прямая.
Эта прямая образует с касательной плоскостью угол 63°. Радиус данной сферы — R.
Вырази через R расстояние данной точки до поверхности сферы.

(Введи округлённый до сотых ответ.)

Answer 1

Ответ:≈ 0,122•R

Объяснение:

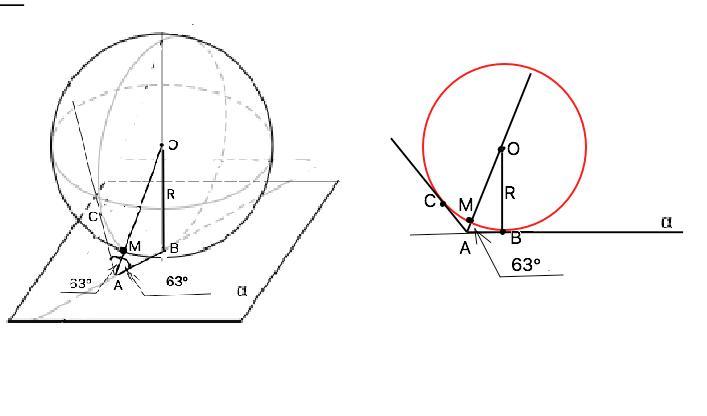
На рисунке вложения сфера касается плоскости  α,   справа дан схематический рисунок к задаче.

  Точка А лежит на плоскости вне сферы, АО - расстояние от т.А до центра сферы, АВ и АС - касательные из А к сфере. Соединим т. А и центр О сферы.

  Радиус ОВ, проведенный в точку касания сферы и плоскости, перпендикулярен плоскости касания, значит, перпендикулярен любой прямой этой плоскости, проходящей через эту точку. Точки А и В лежат на одной касательной, и с центром сферы образуют прямоугольный треугольник АОВ.

 Искомое расстояние АМ - разность между длиной отрезка АО и радиусом сферы.

АО=R:sin 63°,   АМ=R:sin63°- R  

sin63°=0,891

АМ=(R- R•0,891):0,891=0,10899R:0,891=0,122326•R ≈ 0,122•R