Question

Складіть рівняння прямої , зображеної на рисунку

Answer 1

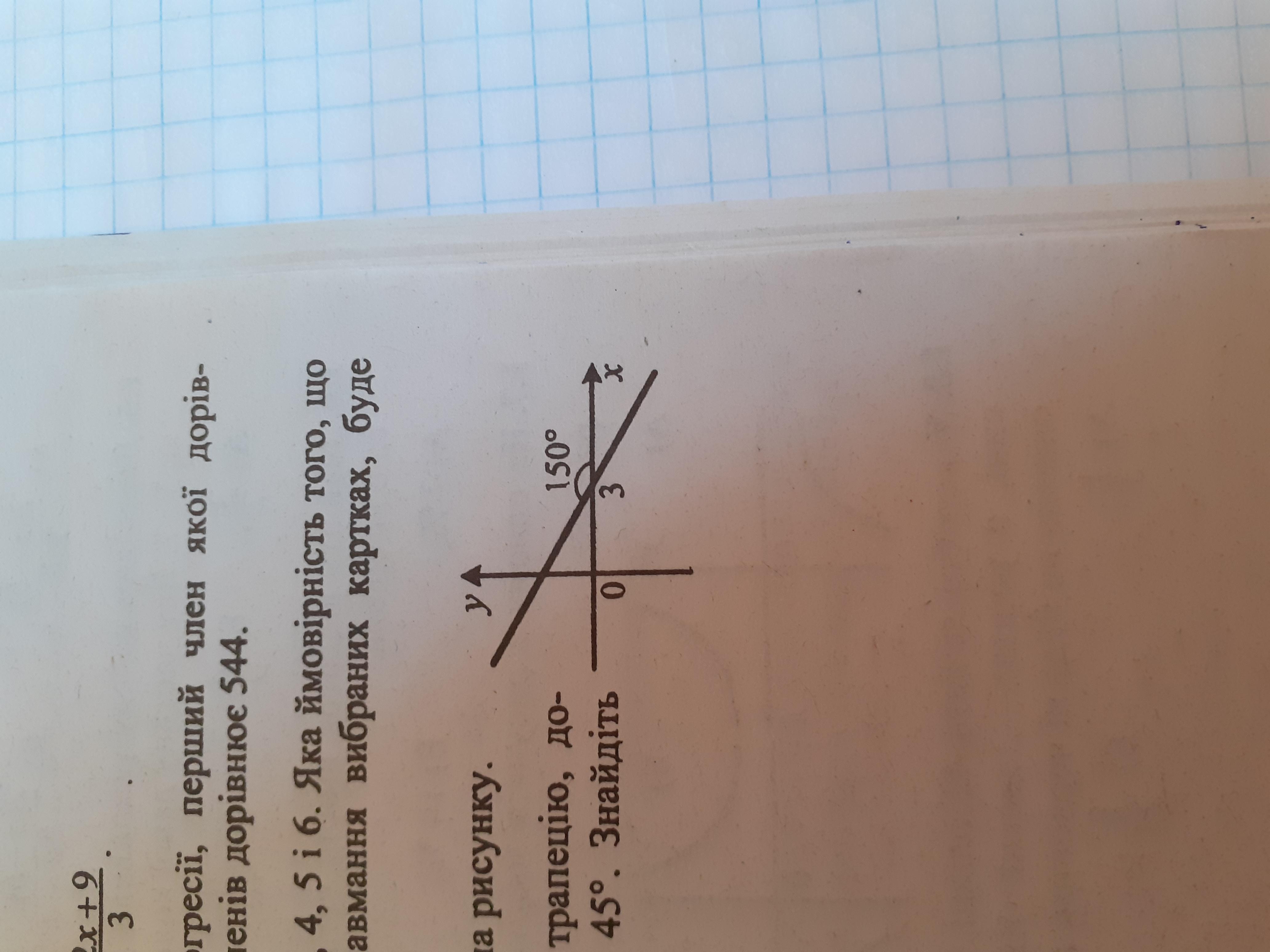
Функція є лінійною, тому її рівняння має вид: $y = kx + b$.

Візьмемо точки, зображені на графіку.

$x = 3, y = 0$

Однак для рівняння нам не вистачає ще одного значення - $b$

Для його знаходження ми використаємо прямокутний трикутник з гострим кутом 30° (180° - 150° = 30°). Коефіцієнт $b$ - то є перетин з віссю $y$

З трикутника: $b = 3 cdot text{tg} 30^{circ} = 3 cdot dfrac{sqrt{3} }{3} = sqrt{3}$

Тепер підставимо всі знайденні вище коефіцієнти в формулу лінійної функції і знайдемо значення $k$:

$0 = 3k + sqrt{3}\3k = -sqrt{3}\ k = -dfrac{sqrt{3}}{3}$

Отже, рівняння прямої має вид: $y = -dfrac{sqrt{3}}{3}x + sqrt{3}$.

Відповідь:  $y = -dfrac{sqrt{3}}{3}x + sqrt{3}$

Answer 2

Спасибо , очень помогли

Answer 3

Не за что!