Question

В треугольник ABC вписана окружность с центром O. Прямая BO вторично пересекает описанную около треугольника ABС окружность в точке P.
1) Докажите, что углы PCO и POCравны.
2) Найдите площадь треугольника APC, если радиус описанной окружности равен 6, а угол ABC = 120 градусов.

Answer 1

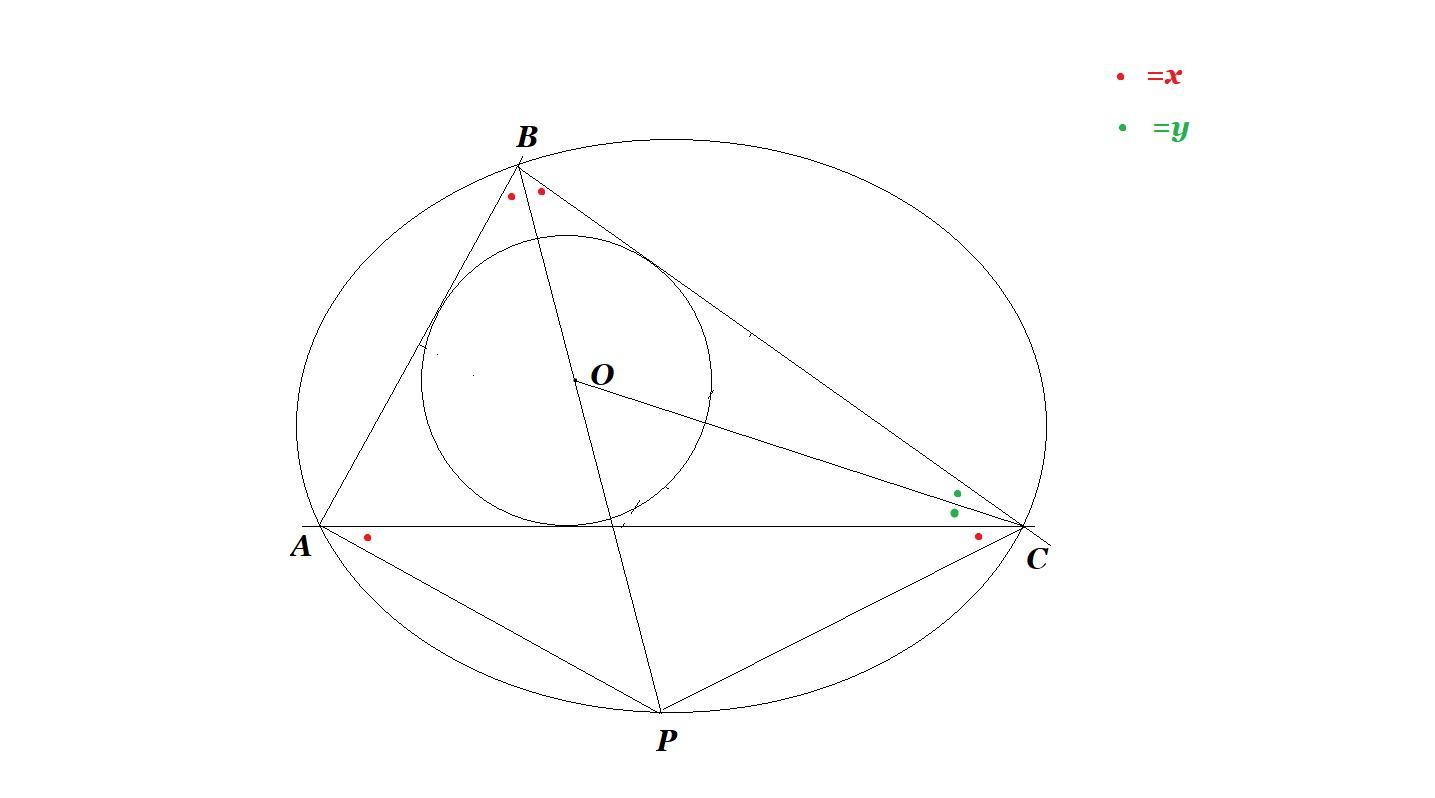
Все обозначения на рисунке.

Углы ABO, CBO равны, т.к. BO - биссектриса, аналогично равны углы BCO и OCA; Дуги AP и PC равны => AP=PC => углы PAC и ACP равны. Угол ABP равен углу ACP, так как они опираются на одну дугу.

1) Выразим через x и y угол PCO: PCO=x+y; Теперь угол POC: POC=180-BOC; BOC=180-x-y => POC=180-(180-x-y)=x+y; Значит PCO=POC что и требовалось.

2) Из доказанного ранее, что не умаляет очевидности этого факта, AP=PC; Так как угол ABC = 120, то угол APC=60; Следовательно треугольник APC является равносторонним. Найдем AC по известной формуле: $AC=2Rsin angle ABC=2times 6times frac{sqrt{3}}{2} =6sqrt{3}$; Площадь треугольника APC: $S=frac{1}{2}times 6sqrt{3}times 6sqrt{3} times frac{sqrt{3}}{2}=frac{36times3sqrt{3}}{4}=27sqrt{3}$