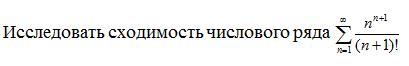Question

Решите, пожалуйста, данный ряд с полным объяснением (Исследовать на сходимость).

Answer 1

Рассмотрите предложенное решение; использовался признак д'Аламбера.

Answer 2

1) одного порядка роста. Предел такого отношения есть 1.

Answer 3

2) В числителе и знаменателе не просто 'n', а степень в степени. Опять-таки, порядок роста у (n+1) выше.

Answer 4

спасибо большое)

Answer 5

И ещё кое-что, я вот заметил что при сокращении в числителе (n+1)! и в знаменателе (n+2)! даёт в знаменателе (n+1). Вопрос: как?
В числителе (n+1)!= n!*(n+1)
В знаменателе (n+2)!= n!*(n+1)*(n+2)
И если это сократить то получится в знаменателе (n+2), а не (n+1)

Answer 6

Это из теории, раздел дроби с факториалами. В комментариях мало места.