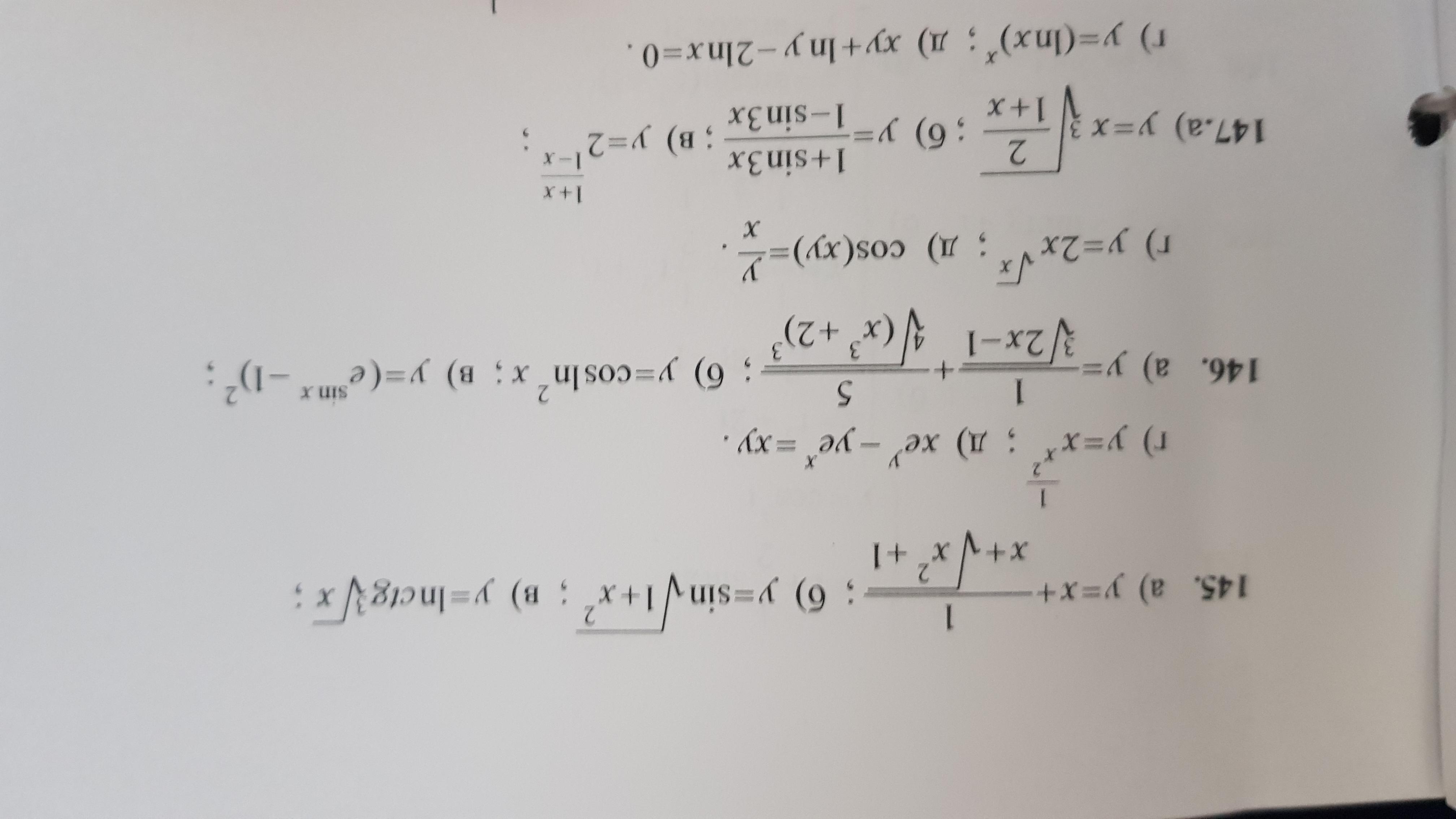Ответы
Ответ дал:
0
Решение во вложении.
Приложения:

Ответ дал:
0
у=2*х в степени х.
пример на логарифмическое дифференцирование.
у/2=х в степени √х, возьмем предварительно логарифм натуральный от обеих частей, получим ㏑(у/2)=㏑(х в степени √х) правая часть по свойству логарифма может быть переписана как √х* (㏑(х))
теперь возьмем производную от обеих частей. помня, что у - сложная функция; а справа производная от произведения;
1/(у/2)*у штрих=(1/(2√х))*(㏑(х))+√х/х
2у штрих/у=(㏑(х))/(2√х)+(√х/х)
у штрих равен (у/2)*((㏑(х))/(2√х)+(√х/х)), подставим вместо у данное в условии выражение, получим ответ.
у штрих =((2/2)*х в степени √х)*((㏑(х))/(2√х)+(√х/х))
у штрих =( х в степени √х)*((㏑(х))/(2√х)+(√х/х))
Приложения:

Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад