Question

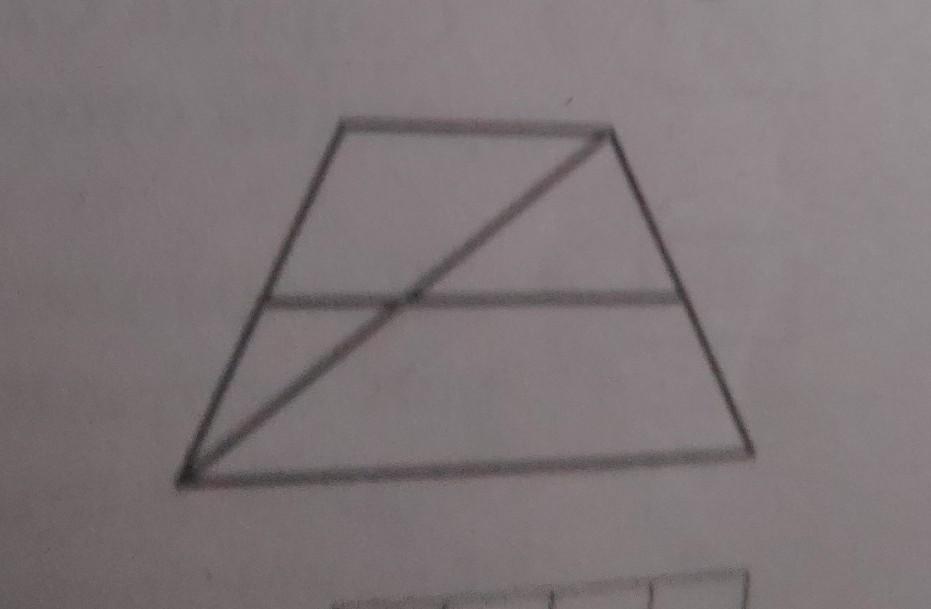
основание трапеции равны 10 и 11 найдите больший из отрезков на которые делит среднюю линию этой трапеции одна из и ее диагоналей. Решение нужно через подобие треугольников по рисунку выше . Помогите ПОЖАЛУЙСТА как МОЖНО СКОРЕЕ!!!​

Answer 1

Ответ:

Объяснение:

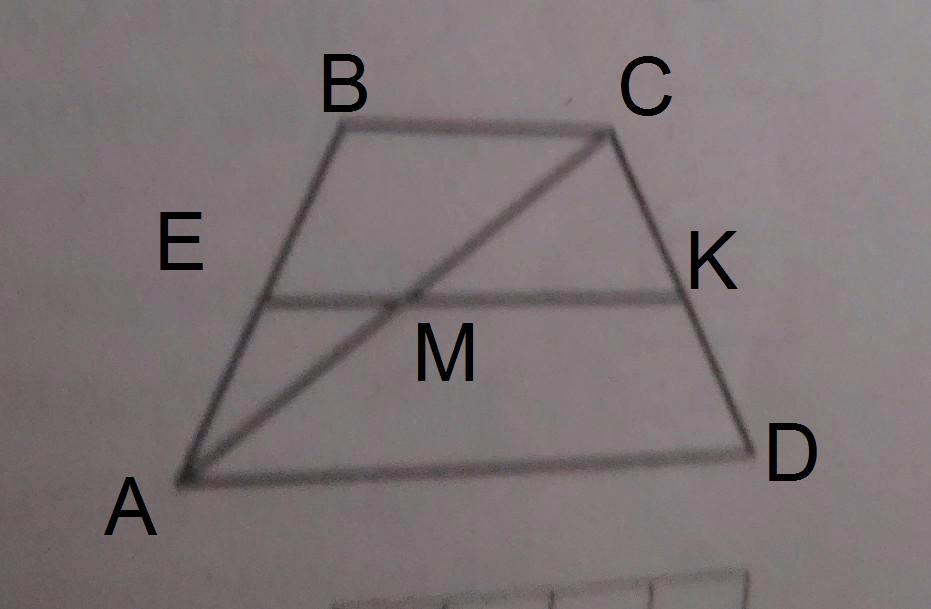
по признаку средней линии треугольника если отрезок параллелен одной стороне треугольника и проходит через середину другой стороны то он является средней линией.

⇒ MK -средняя линия треугольника АСD

MK=AD/2=11/2=5.5

Answer 2

Т.к. большее основание, пусть это будет АВ,  параллельно средней линии, например,  КТ, и средняя линия пересекается с диагональю АС, например, в точке О, где Т принадлежит боковой стороне ВС, тогда ОТ║АВ, а, значит, треугольники СОТ и САВ подобны по 1 признаку  подобия, т.е. по двум углам,  т.к. углы СОТ и САВ равны как соответственные при параллельных ОТ и АВ и секущей АС, угол С у них общий, тогда ОТ/АВ=СТ/СВ=1/2, значит, ОТ=АВ/2=11/2=5.5