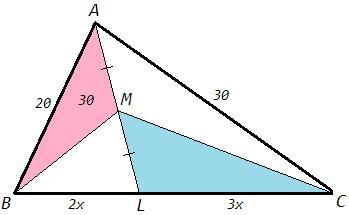
Точка M — середина биссектрисы AL треугольника ABC. Известно, что AB=20, AC=30, а площадь треугольника ABM равна 30. Найдите площадь треугольника MLC
Приложения:
Ответы
Ответ дал:
0
По теореме о биссектрисе
BL/CL =AB/AC =20/30 =2/3
Треугольники BAL и CAL имеют общую высоту (перпендикуляр из вершины A к BC), следовательно их площади относятся как основания.
S(BAL)/S(CAL) =BL/CL =2/3
Треугольники ABM и MBL имеют общую высоту и равные основания (AM=ML), следовательно их площади равны.
S(ABM)=S(MBL)
Аналогично S(AСM)=S(MСL)
S(BAL)= 2 S(ABM)
S(CAL)= 3/2 S(BAL)
S(MCL)= 1/2 S(CAL) =1/2 *3/2 *2 *30 =45
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад