Question

Радиус сферы разделен на три равные части и через точки деления проведены перпендикулярные ему плоскости. Найдите площадь сферы если разность длин сечений равна 6(2√2-√5)пи см

Answer 1

Ответ: 324π

Объяснение:

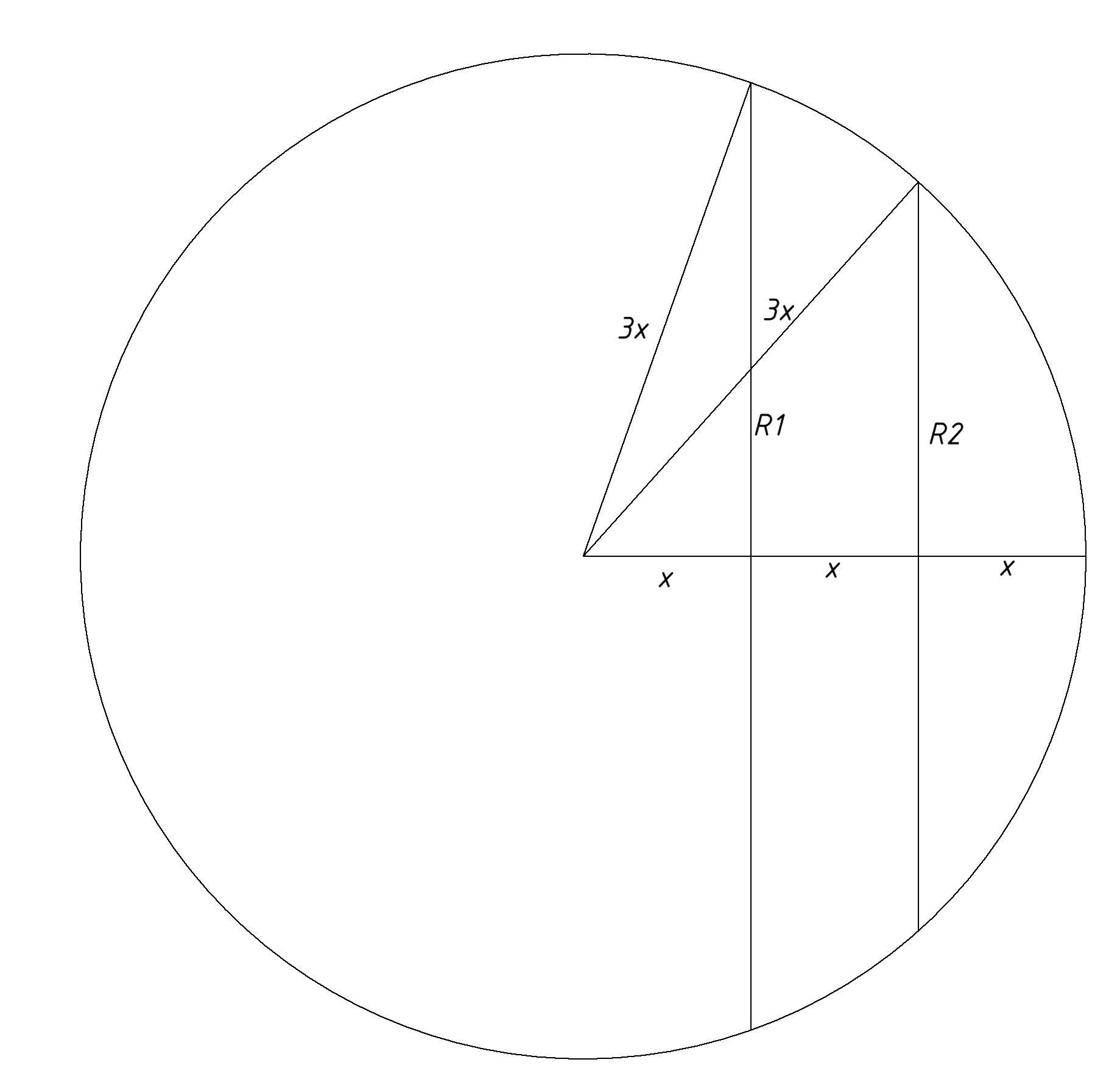
Пусть   плоскости с радиусами R1 и R2   делят радиус сферы на  три равных кусочка длины x. Соответственно радиус сферы R=3x.     Cмотрите рисунок.

По теореме  Пифагора определим  радиусы сфер:

R1^2= ( (3x)^2-(x)^2)= 9x^2-x^2=8*x^2

R1=2√2*x

R2^2= ( (3x)^2 -(2x)^2)= 9x^2 -4x^2=5x^2

R2=√5*x

Определим длины сечений:

L1=2πR1=2π*2*√2*x

L2=2πR2=2π*√5*x

Из условия:

L1 - L2= 6*π*(2√2-√5)

L1 - L2= 2*x*π*(2√2-√5)

Откуда:

6*π*(2√2-√5)=2*x*π*(2√2-√5)

x=3

R=3x=9

Откуда площадь сферы:

S=4*π*R^2=324π

Answer 2

Опечатка. 7 строчка: определим радиуса сечений*