Ответы
Ответ дал:
0
Ответ:
Объяснение:
=============
Приложения:
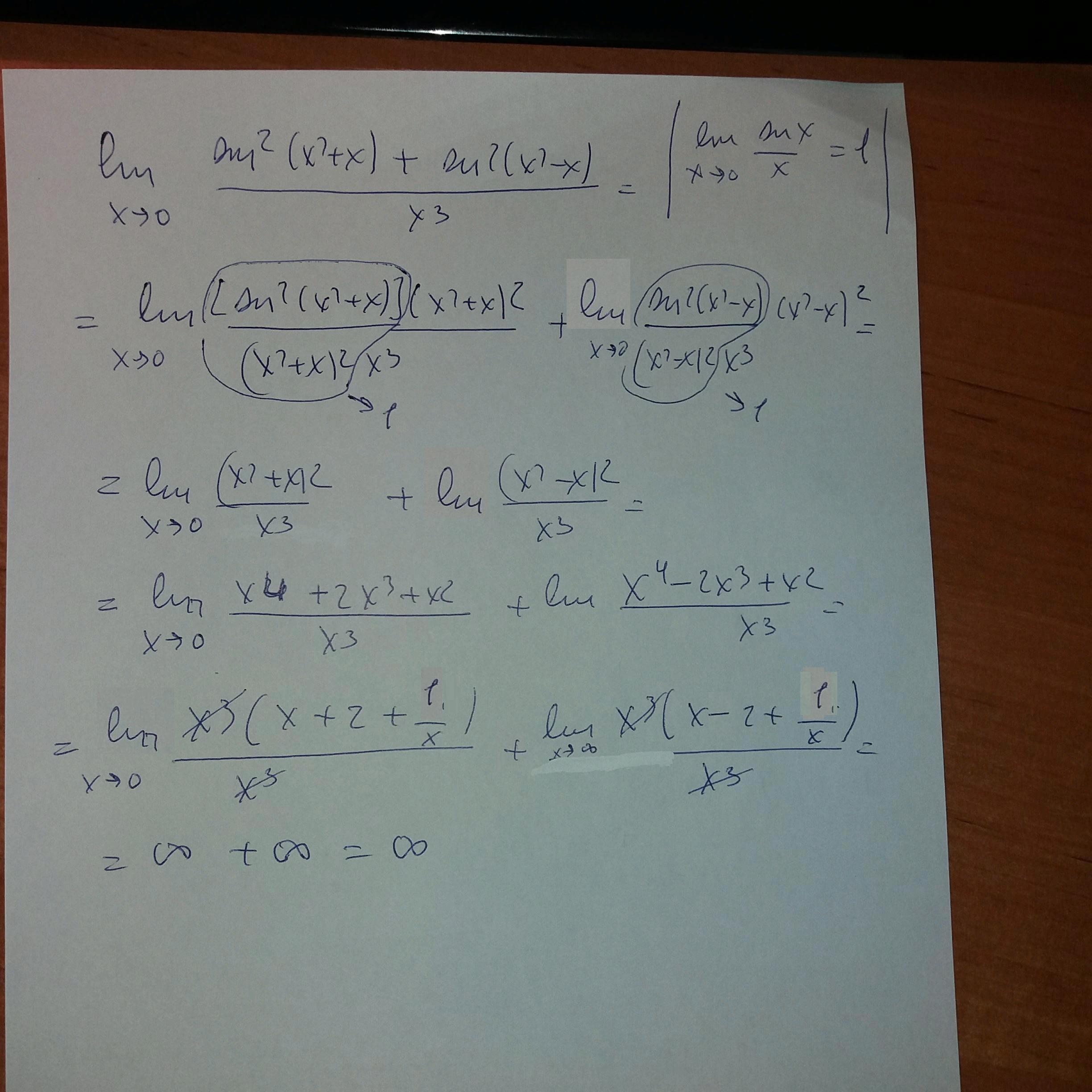
Ответ дал:
0
пример точно не содержал ответа бесконечности?
Ответ дал:
0
звонить и спрашивать в 21 раз бесполезно
Ответ дал:
0
наверняка был
Ответ дал:
0
либо условие не так запомнили и продиктовали
Ответ дал:
0
посмотрим решение еще одного знатока....
Ответ дал:
0
Нужен предел от (sin²(x²+x)+sin(x²-x))/x², т.к. х стремится к нулю, то и х³+х, и х²-х тоже стремятся к нулю, и можем заменить sin(x²+x) эквивалентной величиной (x²+x), а sin(x²-x) величиной (x²-x), тогда сумма их квадратов в числителе перепишется, как х⁴+2х³+х²+х⁴-2х³+х²=2х⁴+2х², а предел от (2х⁴+2х²)/х³ =2/х+2/х² при х стремящемся к нулю равен ∞
Использовал теоремы - сумма конечного числа бесконечно малых есть величина бесконечно малая и принцип замены эквивалентных.
Приложения:
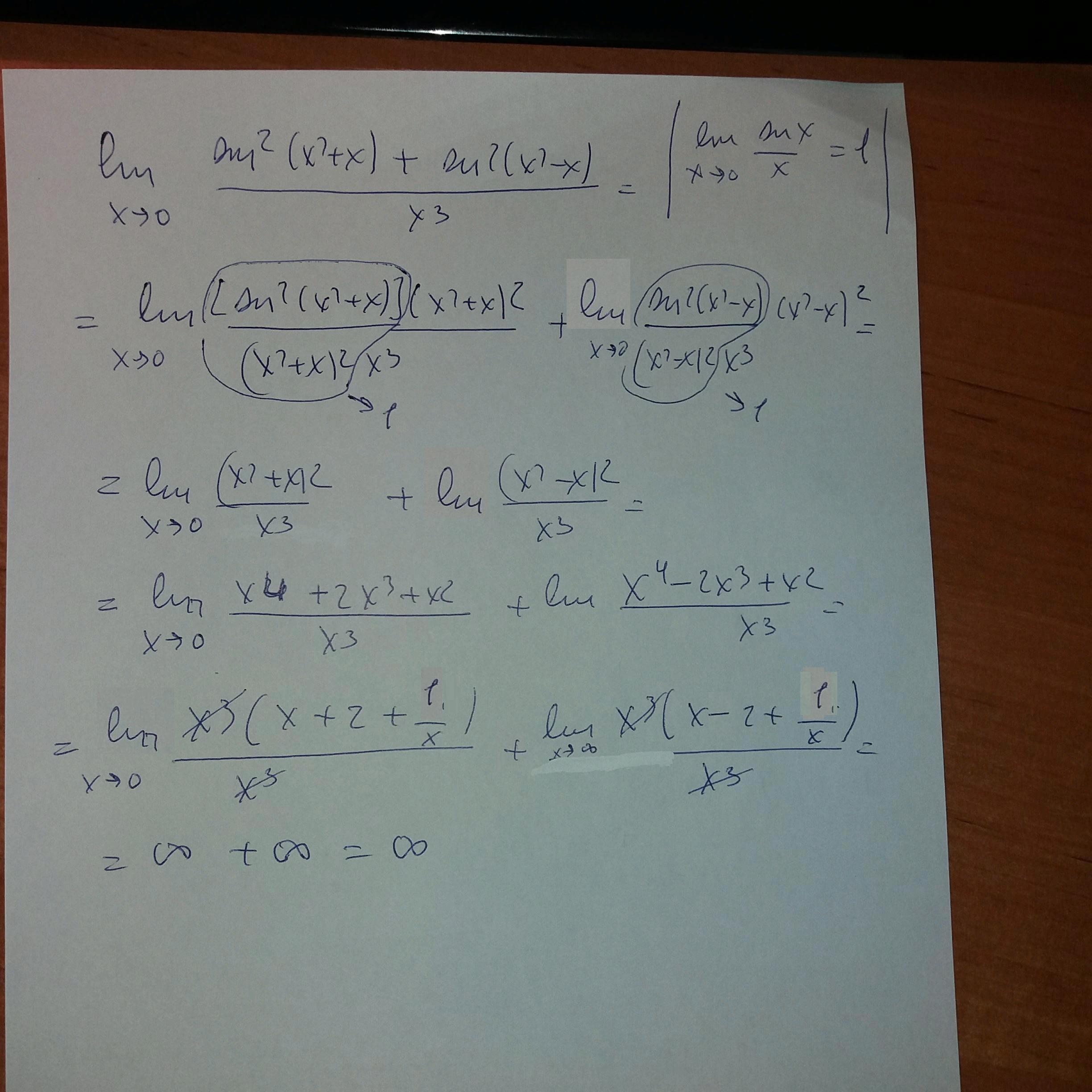
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад