Question

Вычислите площадь области ограниченной кривыми$left { {{y=x} atop {y=x+sin^{2}x }} right. \\0leq xleq pi$

Answer 1

$displaystyleleft { {{y=x} atop {y=x+sin^2x}} right.~~~Leftrightarrow~~~left { {{y=x} atop {y=x+dfrac{1-cos(2x)}2}} right.\\\left { {{y=x} atop {y=x+dfrac 12-dfrac{cos(2x)}2} right.$

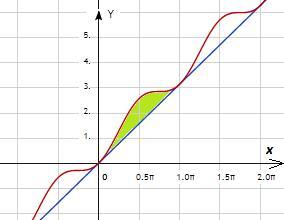
y = x   - линейная функция, график которой проходит через начало координат.  y(0) = 0;  y(π) = π

у = x + sin²x   -  график функции  - синусоида, которая колеблется над прямой y=x, касаясь прямой.  y(0) = 0;  y(π)=π+sin²π=π

Точки пересечения графиков на заданном интервале  x₁=0;  x₂=π

$displaystyleintlimits^{pi}_0 {Big(x+dfrac 12-dfrac{cos(2x)}2-x}Big) , dx =intlimits^{pi}_0 {Big(dfrac 12-dfrac{cos(2x)}2}Big) , dx =\\=dfrac x2-dfrac{sin(2x)}4Big|^{pi}_0=dfrac {pi}2-dfrac{sin(2pi)}4-Big(dfrac 02-dfrac{sin 0}4Big)=$

$boldsymbol{=dfrac {pi}2}~~approx 1,57$