Question

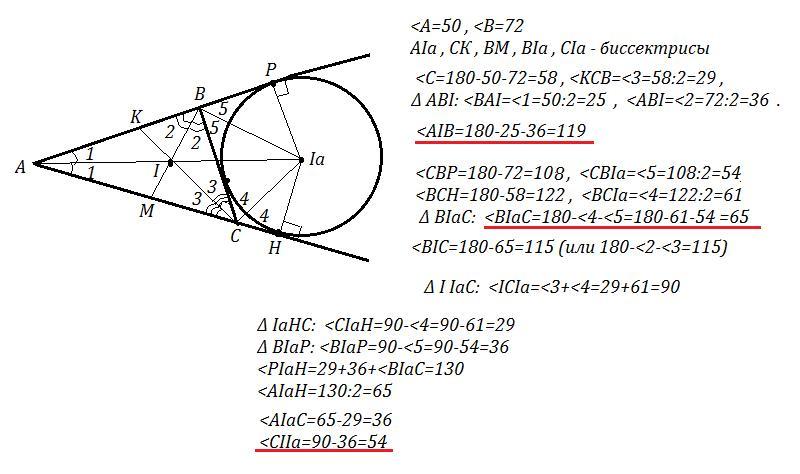
В треугольнике ABC точка I — центр вписанной окружности, точка Ia — центр вневписанной окружности, касающейся стороны BC. Известно, что ∠A=50∘, ∠B=72∘. Вычислите величины следующих углов.

∠AIB ∠BIaC ∠CIIa​

Answer 1

Центр вписанной в треугольник окружности лежит на пересечении биссектрис этого треугольника.

Центр вневписанной окружности лежит на пересечении биссектрис внешних углов треугольника и биссектрисы внутреннего угла тр-ка, лежащего против стороны, которой касается вневписанная окружность.

Значит точки  $A; ,; I; ,; Ia$  лежат на одной и той же биссектрисе.

Answer 2

завтра попробую

Answer 3

там вроде через день после ответа можно

Answer 4

nnnLLL через какую программу так рисуете?

Answer 5

через Paint

Answer 6

спасибо