Question

q(x)=x⁵- 5x³ исследовал при помощи производной и построить график функций

Answer 1

$Q(x)=x^5-5x^3$

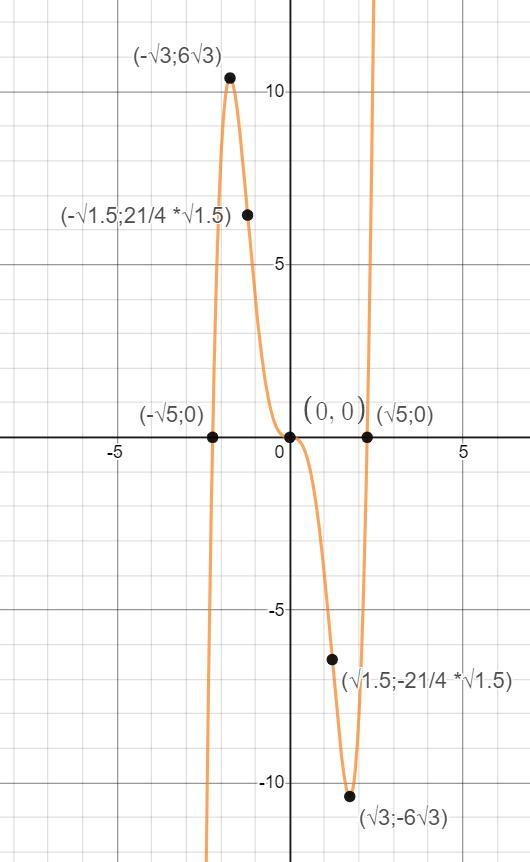
Для начала найдём точки пересечения с осями координат.

$Q(0)=0^5-5*0^3=0,(0;0)\Q(x)=x^5-5x^3=x^3(x^2-5)=0\(-sqrt{5};0),(0;0),(sqrt{5};0)$

Функция нечётная т.к. Q(x)= -Q(-x)

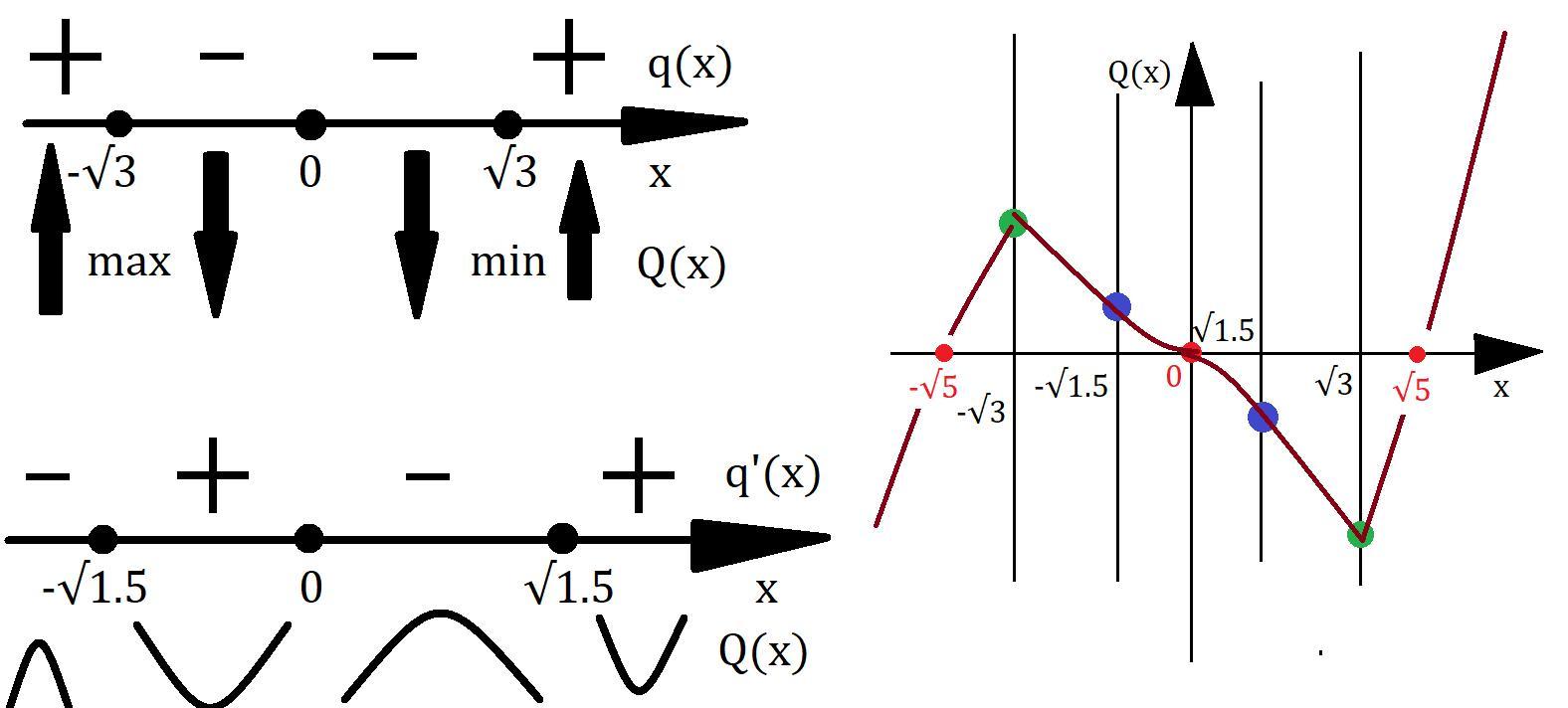
Исследуем функцию на возрастание, убывание и экстремумы.

$Q'(x)=q(x)=5x^4-15x^2=5x^2(x^2-3)=\5x^2(x-sqrt{3})(x+sqrt{3})\Q(0)=0\Q(-sqrt{3})=-9sqrt{3}+15sqrt{3}=6sqrt{3}\Q(sqrt{3})=-6sqrt{3}$

Смотри вниз.

Исследуем функцию на выпуклость вверх, вниз и точки перегиба.

$Q''(x)=q'(x)=20x^3-30x=20x(x^2-1.5)=\x(x-sqrt{1.5})(x+sqrt{1.5})\Q(0)=0\Q(-sqrt{1.5})=-frac{9}{4}sqrt{1.5}+frac{15}{2}sqrt{1.5}=frac{21}{4}sqrt{1.5}\Q(sqrt{1.5})=-frac{21}{4}sqrt{1.5}$

Смотри вниз.

$6sqrt{3}Vfrac{21}{4}sqrt{1.5};24^2*3V21^2*1.5;576>147*1.5$

У нас есть всё, чтобы построить график функции.