Ответы
Ответ дал:
0
Для начала введём единичную окружность и отметим углы α и β, α > β. Отметим также векторы a и b, которые образуют углы α и β соответственно.
Вспомним, что скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними, а этот угол равняется α-β. Длины этих векторов равны 1, так как являются радиусами единичной окружности, а произведение этих векторов в координатах равно . Но мы знаем, что x – это косинус угла, а y – синус. Тогда
. Заменив x и y на косинусы и синусы, получим известную формулу косинуса разности.
Приложения:
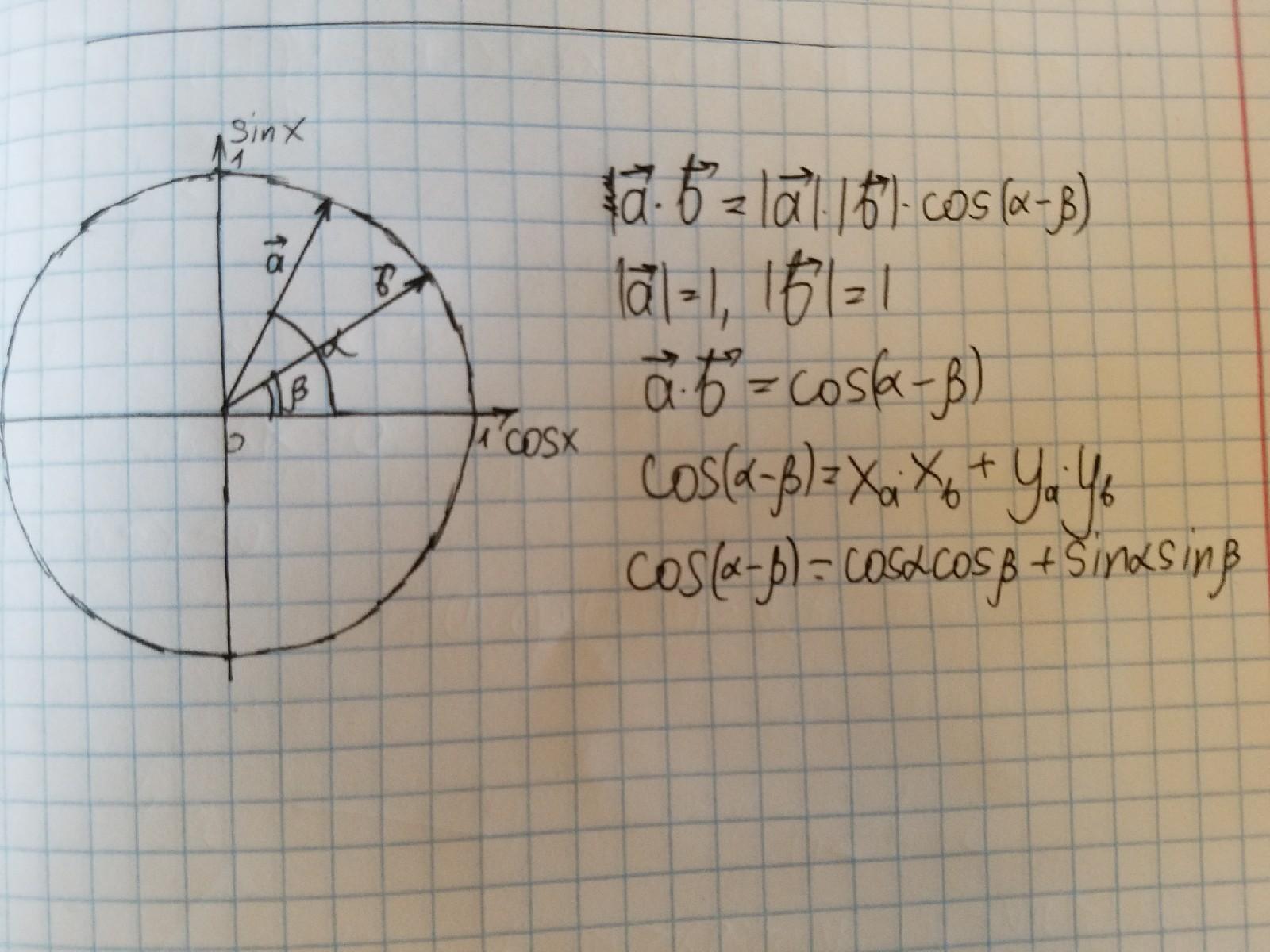
Ответ дал:
0
Доказательство во вложении :
Приложения:

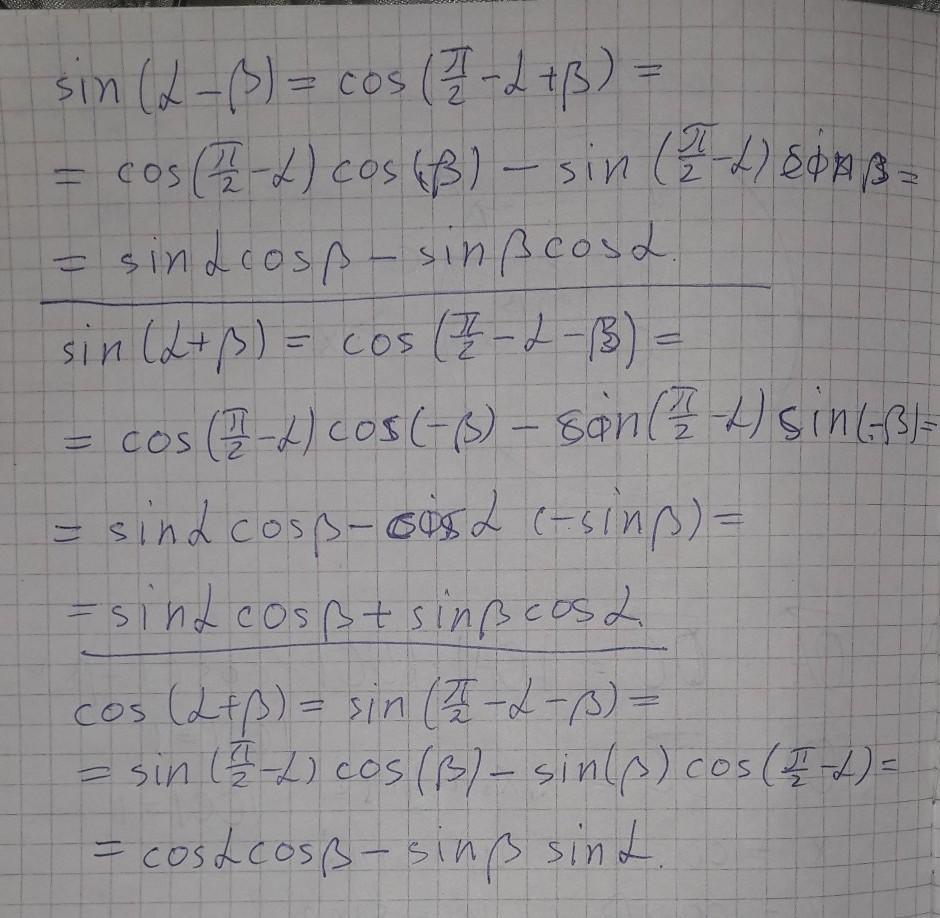
Ответ дал:
0
спасибо
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
9 лет назад