Question

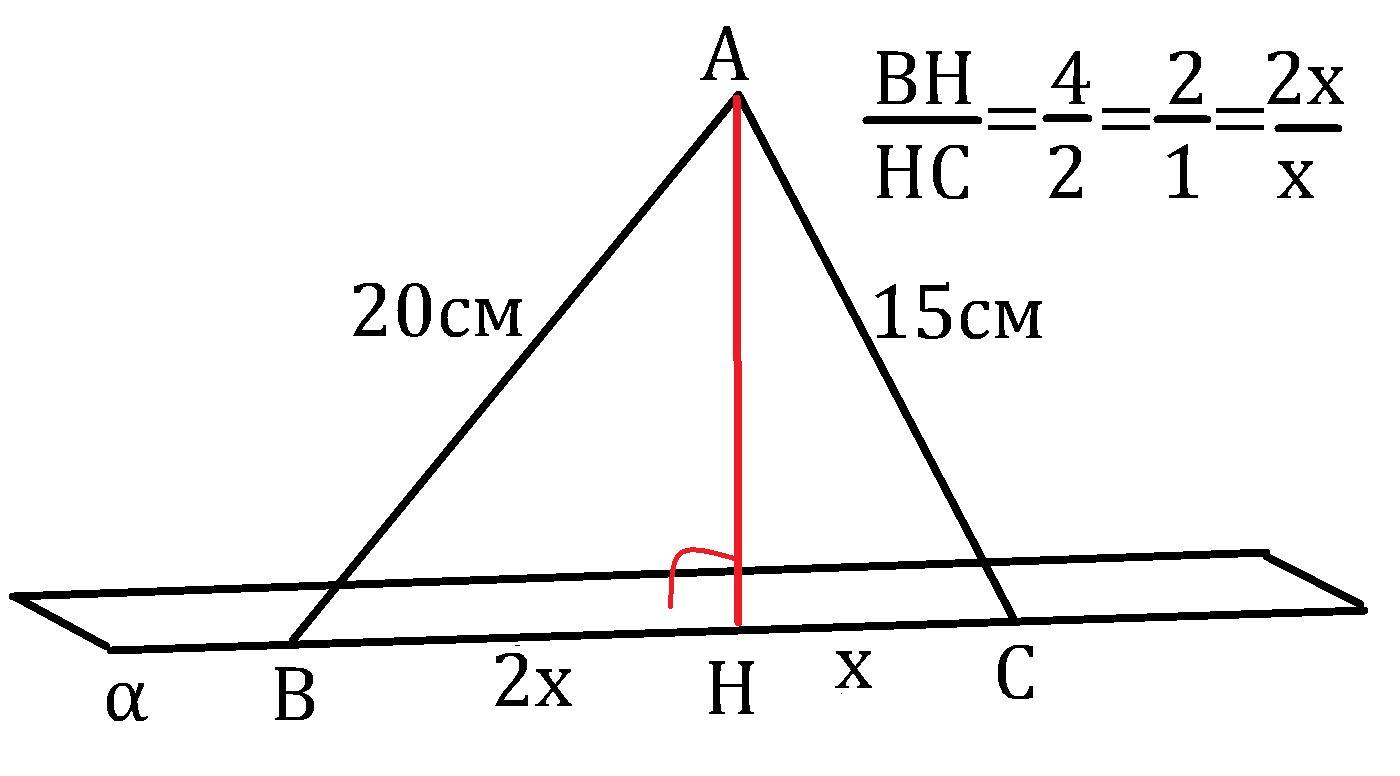
Из точки A лежащей вне плоскости альфа, проведены две наклонные АВ=20см и АС=15см. Их проекции относятся как 4:2 соответственно. Найдите расстояние то точки А до плоскости альфа.

Answer 1

AH⊥α, H∈α ⇒ ρ(A;α) = AH.

В прямоугольном ΔAHB: AH² =AB² -BH² =400 см² -4х².

В прямоугольном ΔAHC: AH² =AC² -CH² =225 см² - х².

Значит:

400 см² -4х² =225 см² - х² ;

175 см²=3x²

$x^2=frac{175}{3}cm^2\AH^2=225cm^2-frac{175}{3}cm^2=frac{675-175}{3}cm^2=frac{500}{3}cm^2\AH=10sqrt{frac{5}{3}}cm=frac{10sqrt{15}}{3}cm\\Otvet!!:;frac{10sqrt{15}}{3}cm.$