На осі абсцис знайти таку точку М, відстань від якої до точки N(1;-6) була рівною 10.
Заздалегідь дякую.
Ответы
Ответ дал:
0
Комментарий к решению:
Если точка принадлежит оси абсцисс, то её координата по оси ординат всегда 0, я сделал замену переменными для неизвестных координат, x координата по оси абсцисс, y - по оси ординат.
Дальше по теореме Пифагора (в прямоугольном треугольнике), я через катеты выразил гипотенузу (расстояние), которое равно 10 и решил получившиеся уравнение, смотри вниз.
Приложения:
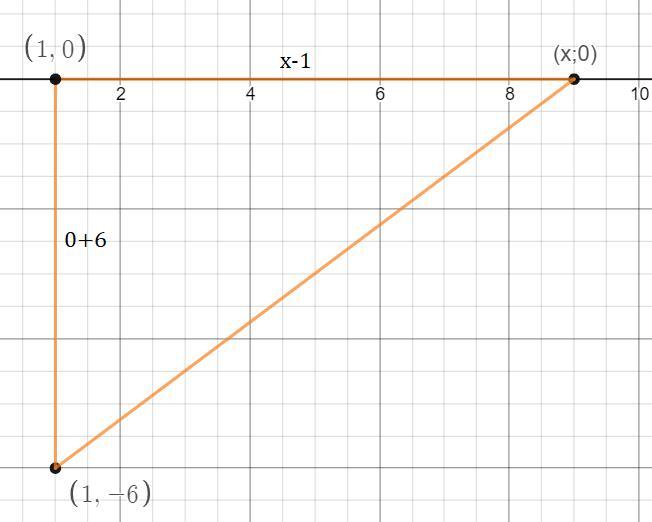
Ответ дал:
0
Если не понятно, то могу на русском объяснить
Ответ дал:
0
Хорошо, объясни пожалуйста
Ответ дал:
0
Точка, лежащая на оси абсцисс имеет ординатой у=0, значит, ищем точку (х;0). Расстояние от нее до точки N(1;-6) равно 10. Квадрат расстояния от искомой точки до точки N равен (1-х)²+(-6-0)²=10²; 1-2х+х²+36=100;
х²-2х-63=0; По теореме, обратной теореме Виета, х₁=9; х₂=-7
Получили аж две точки на расстоянии 10 до точки N(1;-6), это (9;0) и (-7;0)
Ответ (9;0) и (-7;0)
Приложения:

Вас заинтересует
2 года назад
3 года назад
10 лет назад