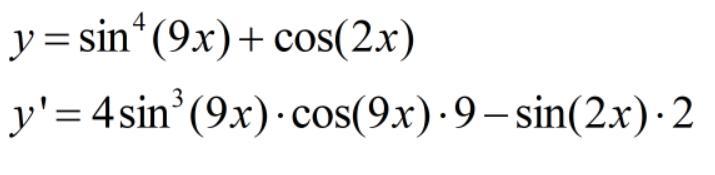Question

y=sin^4(9x)+cos2x срочно памагити найти ппоизврдную​

Answer 1

Чтобы научиться решать производные, нужно сначала научится разбивать выражение на внешние и внутренние функции, и брать производные сначала от внешних, а потом от внутренних функций. Например:

sin^4(9x) -> (sin(9x))^4

Здесь возведение в степень - внешняя функция, затем идет синус, затем - аргумент синуса. Нужно последовательно брать от них производные, при этом перемножая результаты так, как показано ниже:

Answer 2

решишь ещё одну?

Answer 3

Давай

Answer 4

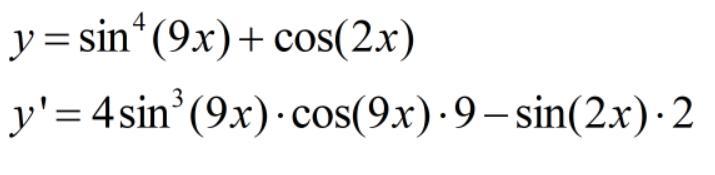
y'=(sin⁴(9x)+cos2x)'=

4*(sin³(9x))*(sin(9x))')-sin((2x))*(2x)'=4*(sin³(9x))*(cos(9x))*(9x)'-sin((2x))*(2x)'=4*9(sin³(9x))(cos(9x))-sin((2x))*(2)=

36*(sin³(9x))*cos(9x))-2sin((2x))

При решении использовал формулу для нахождения сложной функции, для первого слагаемого сначала находим производную от степенной, потом от тригонометрической, потом от линейной функций, и все это перемножал.)  А производная второго слагаемого равна произведению производной тригонометрической функции на производную линейной.