Радиус окружности, описанной вокруг основания правильной
четырехугольной пирамиды, равен 32 см, а апофема – 5 см. Найти
площадь боковой поверхности пирамиды.
Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
Решение дано на фото.
Приложения:
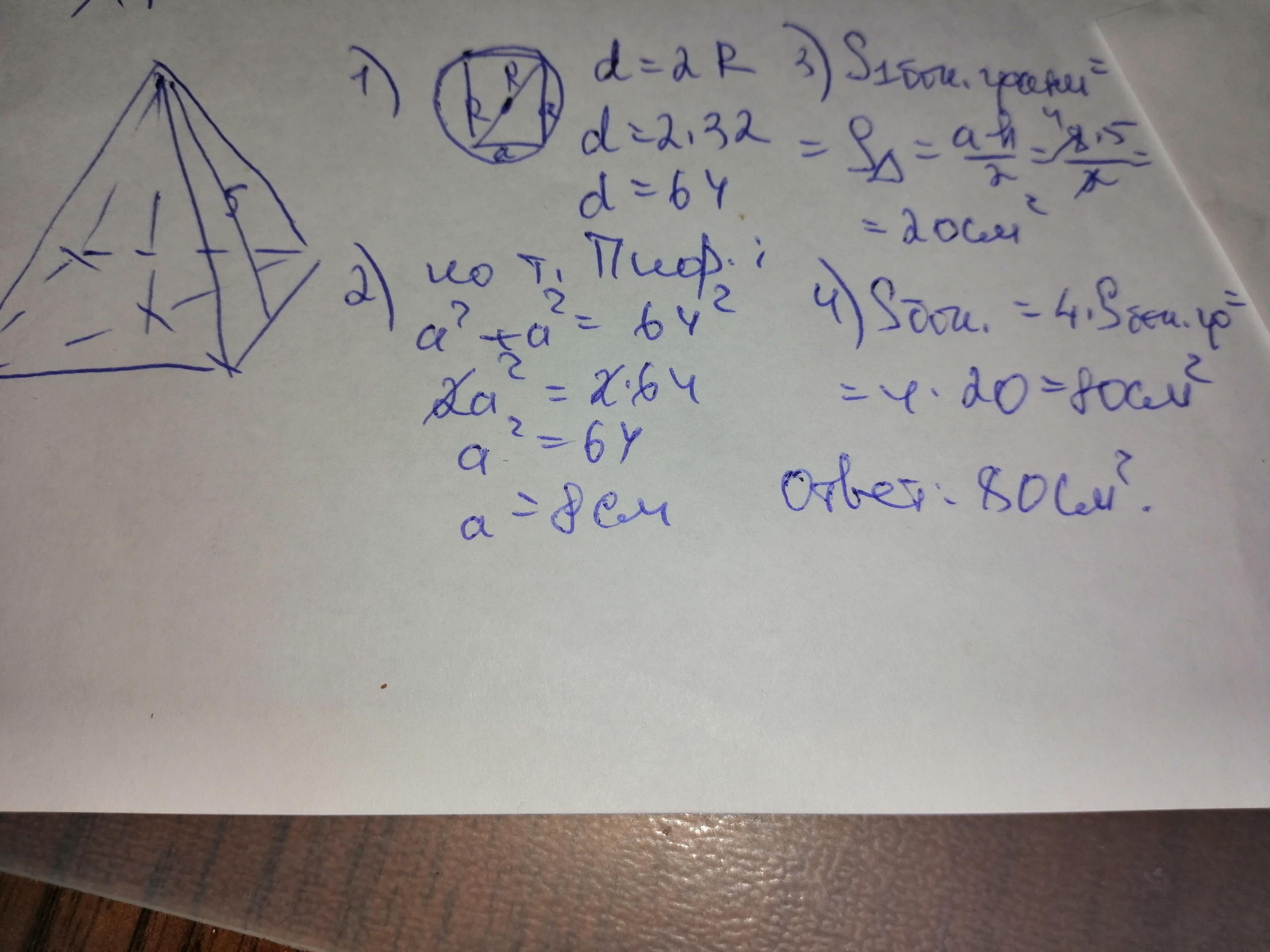
Ответ дал:
0
Основание правильной четырёхугольной пирамиды — квадрат.
Радиус описанной окружности квадрата равен половине его диагонали
2r=d
d=32*2
d=64 см
Сторону квадрата можно найти по формуле
a=d/√2
a=64/√2
a=(64√2)/2
a=32√2 см
Площадь боковой поверхности правильной пирамиды находится по формуле:
Sb=1/2*P*L
, где P - периметр основания, L - апофема
Sb=1/2*32√2*4*5
Sb=2*32√2*5
Sb=320√2cm^2
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад