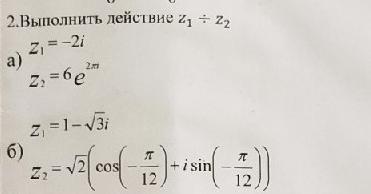Question

Выполнить действие . Алгебра , помогите

Answer 1

a) Преобразуем z2 в алгебраическую форму: $z_2 = 6e^{2pi i} = 6(cos 2pi + isin 2pi) = 6(1+icdot 0) = 6+0i = 6$

Делаем деление и получаем ответ: $frac{z_1}{z_2} = frac{-2i}{6} = -frac{1}{3}i$

б) Преобразуем z1 в тригонометрическую форму:

$r=sqrt{1^2+(sqrt{3})^2} = 2\arg z_1 = varphi = arctan frac{b}{a} = arctan frac{-sqrt{3}}{1} = arctan -sqrt{3} = -frac{pi}{3}\z_1 = 2(cos (-frac{pi}{3}) + isin(-frac{pi}{3}))$

Делаем деление и получаем ответ: $frac{z_1}{z_2} = frac{|z_1|}{|z_2|} (cos (varphi_1-varphi_2) + isin (varphi_1-varphi_2)) = frac{2}{sqrt{2}} (cos (-frac{pi}{3}+frac{pi}{12})+isin (frac{pi}{3}+frac{pi}{12})) = sqrt 2 (cos(-frac{pi}{4})+isin(-frac{pi}{4}))$

Answer 2

a)Представим комплексное число z₂ cначала в тригонометрической, потом в алгебраической форме 6е^(2πi)=6*(cos2π+isin2π)=6;

z₁/z₂=-2i/6=-i/3;

б) z₁=1-√3i  z₂=√2(cos(-π/12)+i*sin(-π/12))

Для числа z₁ найдем модуль и аргумент ; r=√(1+3)=√4=2 α=arctgI-√3/1I=

π/3. Вектор, соответствующий данному числу, лежит в IV четверти, поэтому  одним из аргументов числа  является  угол φ=2π-π/3=5π/3.

z₁=2(cos(5π/3)+isin(5π/3))

z₁/z₂=(2/√2)*cos(5π/3+π/12)+isin(5π/3+π/12))=(√2/2)*cos(7π/4)+isin(7π/4))