Ответы
Ответ дал:
0
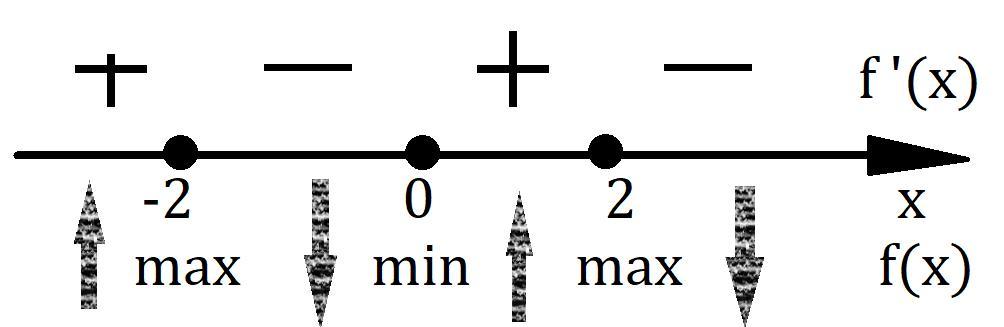
С помощью метода интервалов определим знак производной на разных промежутках, смотри вниз.
Приложения:
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад