Question

Висота трикутника ha дорівнює 12 см, а кути, які прилягають до сторони a, дорівнюють 30 градусів і 45градусів. Чому дорівнює площа цього трикутника?

Answer 1

2. Розглянемо трикутник BHC : кут Н = 90°, кут С=45° отже кут В = 180 - 90 - 45 = 45° => ВН=НС=12см

$s = frac{1}{2} times 12 times (12 + 12 sqrt{3} ) = frac{1}{2} 144 + 144 sqrt{3} = 72 + 144 sqrt{3}$

Answer 2

надіюсь все вірно

Answer 3

Здравствуйте, можете помочь с алгеброй?

Answer 4

да

Answer 5

Можете помочь завтра с ср?

Answer 6

ср?

Answer 7

Ответ:

196,8 см²

Объяснение:

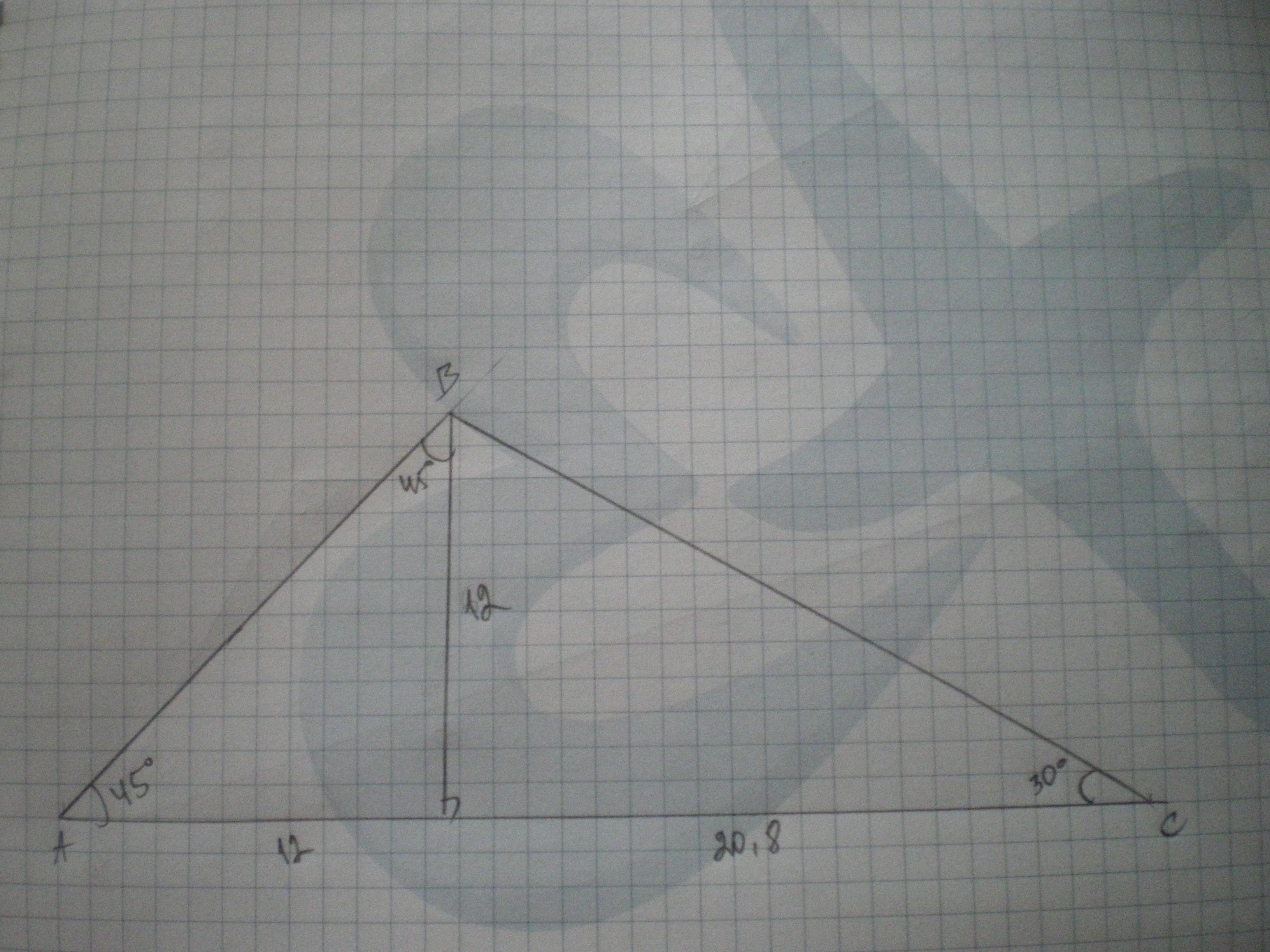
Дано: ΔАВС, ∠А=45°, ∠С=30°, ВН - висота, ВН=12 см.

Знайти S(ABC).

Розглянемо ΔАВН - прямокутний.  ∠АВН=90-45=45°, отже ΔАВН - рівнобедрений, АН=ВН=12 см.

Розглянемо ΔВСН - прямокутний, ВН=12 ВС як катет, що лежить навпроти ∠30°, ВС=12*2=24 см.

СН=√(ВС²-ВН²)=√(576-144)=√432≈20,8 см

АС=12+20,8=32,8 см.

S=12 * АС * ВН = 12 * 12 * 323,8 = 196,8 см²

Answer 8

Здравствуйте, можете помочь с алгеброй?