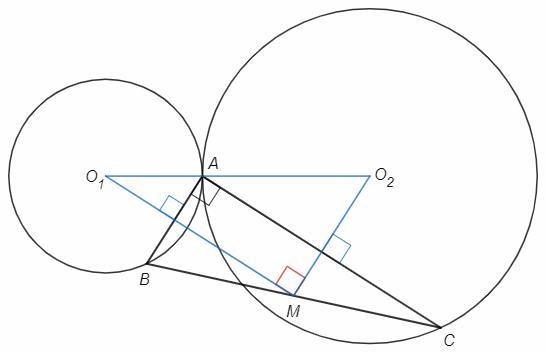
Даны две окружности, касающиеся внешним образом в точке A. В этих окружностях проводятся взаимно перпендикулярные хорды AB и AC. Найдите множество середин гипотенуз получающихся прямоугольных треугольников ABC.
Ответы
Ответ дал:
0
Проведем перпендикуляры из центров к хордам. Перпендикуляр из центра окружности к хорде проходит проходит через ее середину. Перпендикуляры будут являться средними линиями в треугольнике ABC (параллельны основанию, проходят через середину стороны) и пересекутся в середине гипотенузы (M). Треугольник O1MO2 - прямоугольный, точка M лежит на окружности диаметром O1O2.
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад