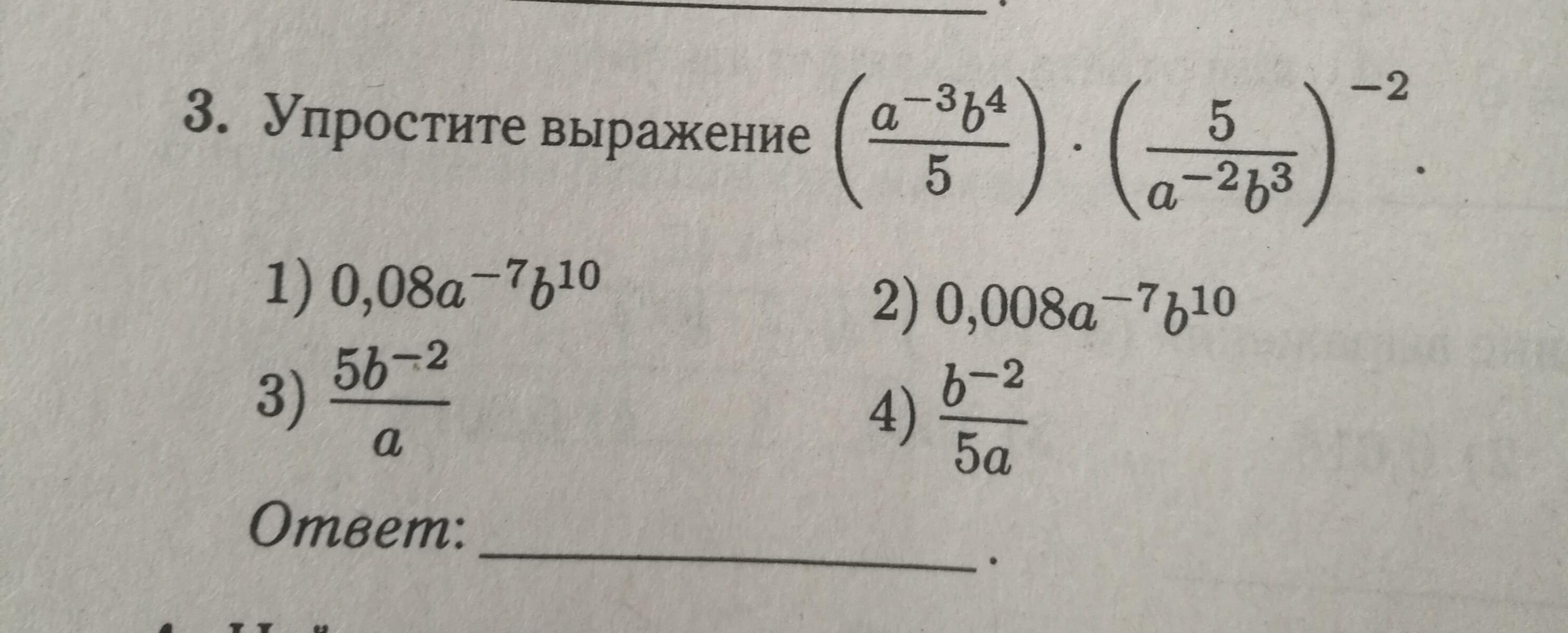Ответы
Ответ дал:
0
Правила:
Решение:
Ответ: 2
Ответ дал:
0
Спасибо!! А как получилось 0,008?
Ответ дал:
0
Деление 1 на 125
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад