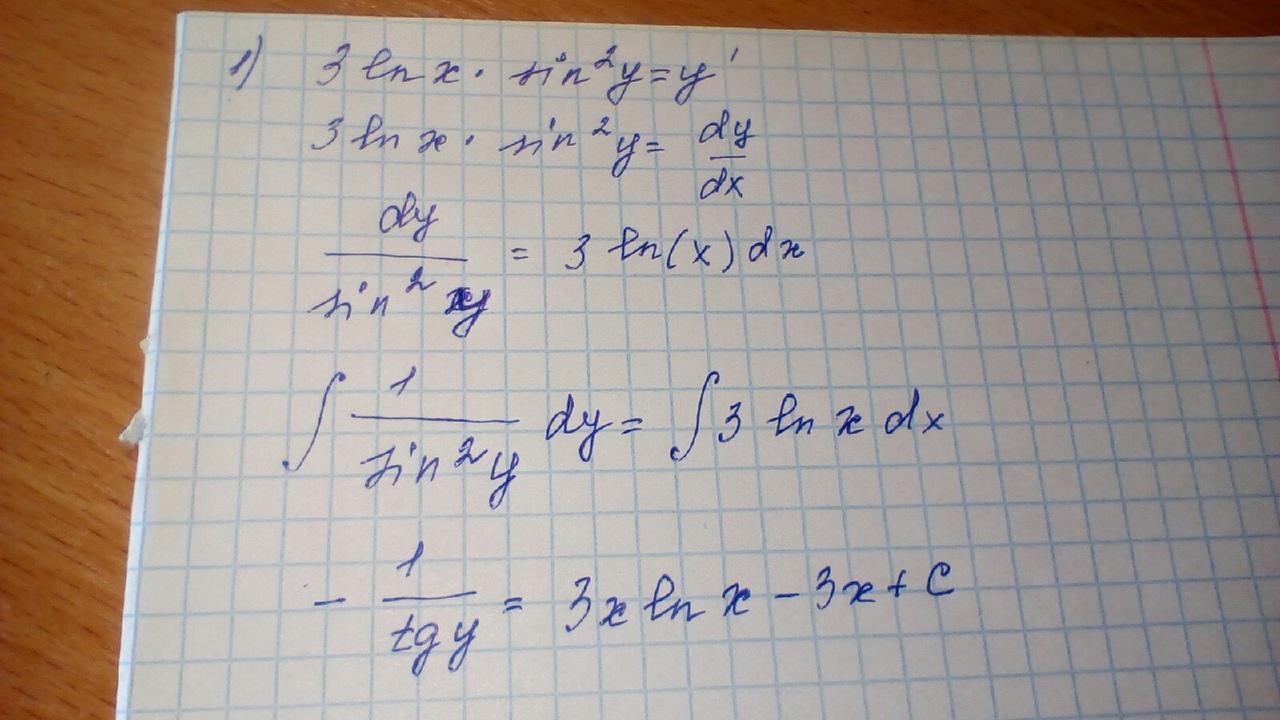Question

3ln(x)*sin^2(y)=y' пожалуйста,горю у меня решено так
не подходит

Answer 1

Это уравнение с разделяющимися переменными.

$dfrac{dy}{dx}=3ln xsin^2y~~~Rightarrow displaystyle intdfrac{dy}{sin^2y}=int3ln xdx$

Посчитаем интеграл правой части уравнения по частям

$displaystyle int3ln xdx=left{begin{array}{ccc}du=dfrac{dx}{x}~~~ u=ln x\ \ dx=dv;~~~ v=xend{array}right}=3xln x-3int xcdot dfrac{dx}{x}=\ \ \ =3xln x-3int dx=3xln x-3x+C$

Мы получим:

$-{rm ctg}, y=3xln x-3x+C~~~Rightarrow~~~ boxed{y={rm arcctg}left(3x-3xln x+Cright)}$

Answer 2

Решение исправил

Answer 3

3㏑х*sin²у=y' - это уравнение с разделяющимися переменными. Разделим переменные. 3㏑х*sin²у=dy/dx⇒ 3㏑хdx=dy/sin²у;

∫3㏑хdx=∫dy/sin²у

Возьмем интеграл от левой части. Будем интегрировать по частям по формуле ∫udv=u*v-∫vdu; ∫㏑хdx, здесь u=㏑x⇒du=dx/x; dv=dx⇒v=x.

∫3㏑хdx=3*∫㏑хdx=3*(x*㏑x-∫x*dx/x)=3*(x*㏑x-x)+c₁

Справа табличный интеграл dy/sin²у=-сtgy+c₂

3*(x*㏑x-x)+c₁=-сtgy+c₂⇒сtgy=c₂-c₁-3*(x*㏑x-x)

y=arcctg((c-3*(x*㏑x-x)); c=-c₁+c₂