Ответы
Ответ дал:
0
Этот корень является решением уравнения без оспаривания ОДЗ.
Ответ дал:
0
Условие такое? Решение задания приложено
Приложения:
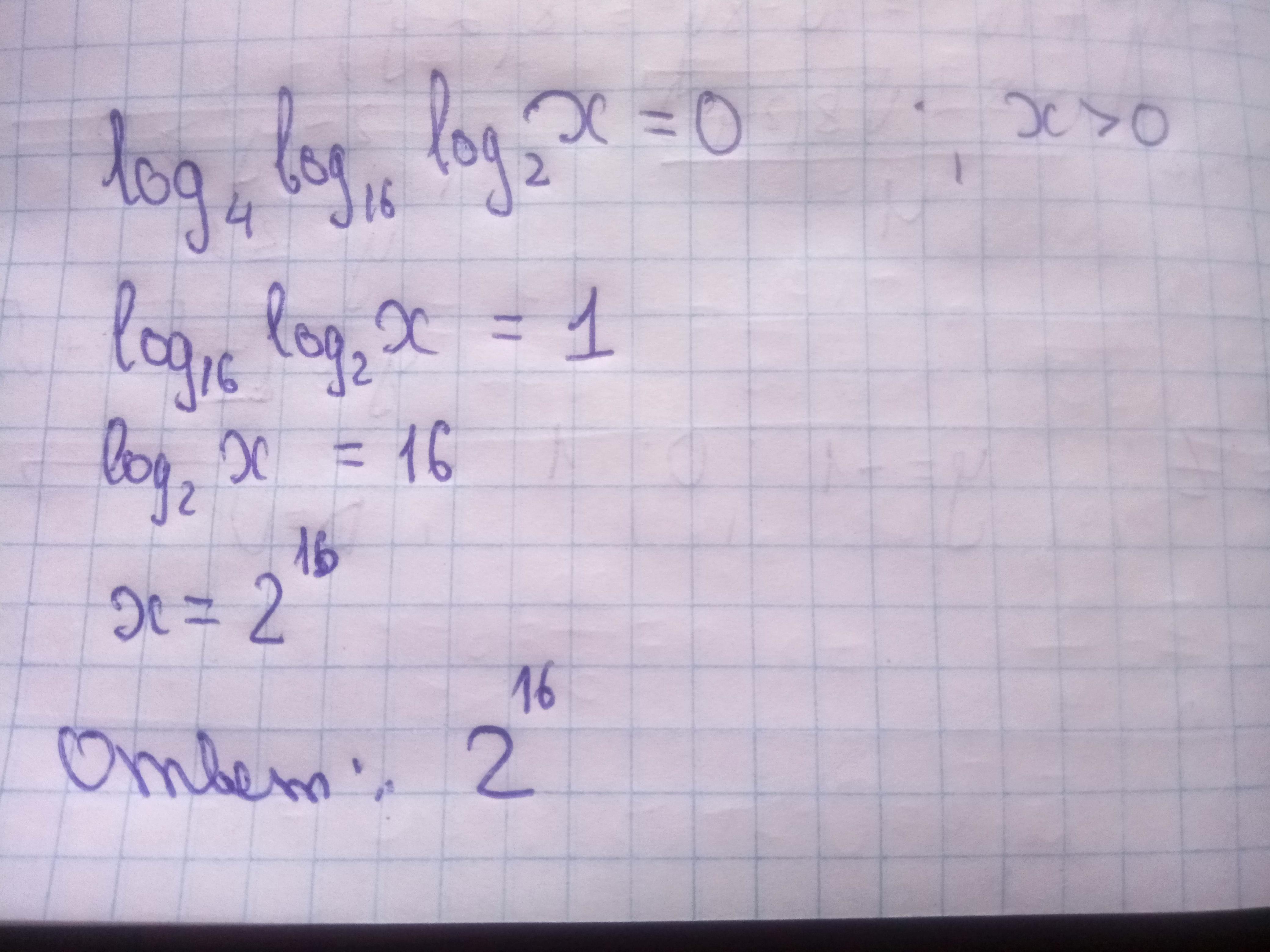
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад