Помогите ребята, спасайте!! Много баллов!
Нужно найти область сходимости степенного ряда, помогите пожалуйста
Приложения:
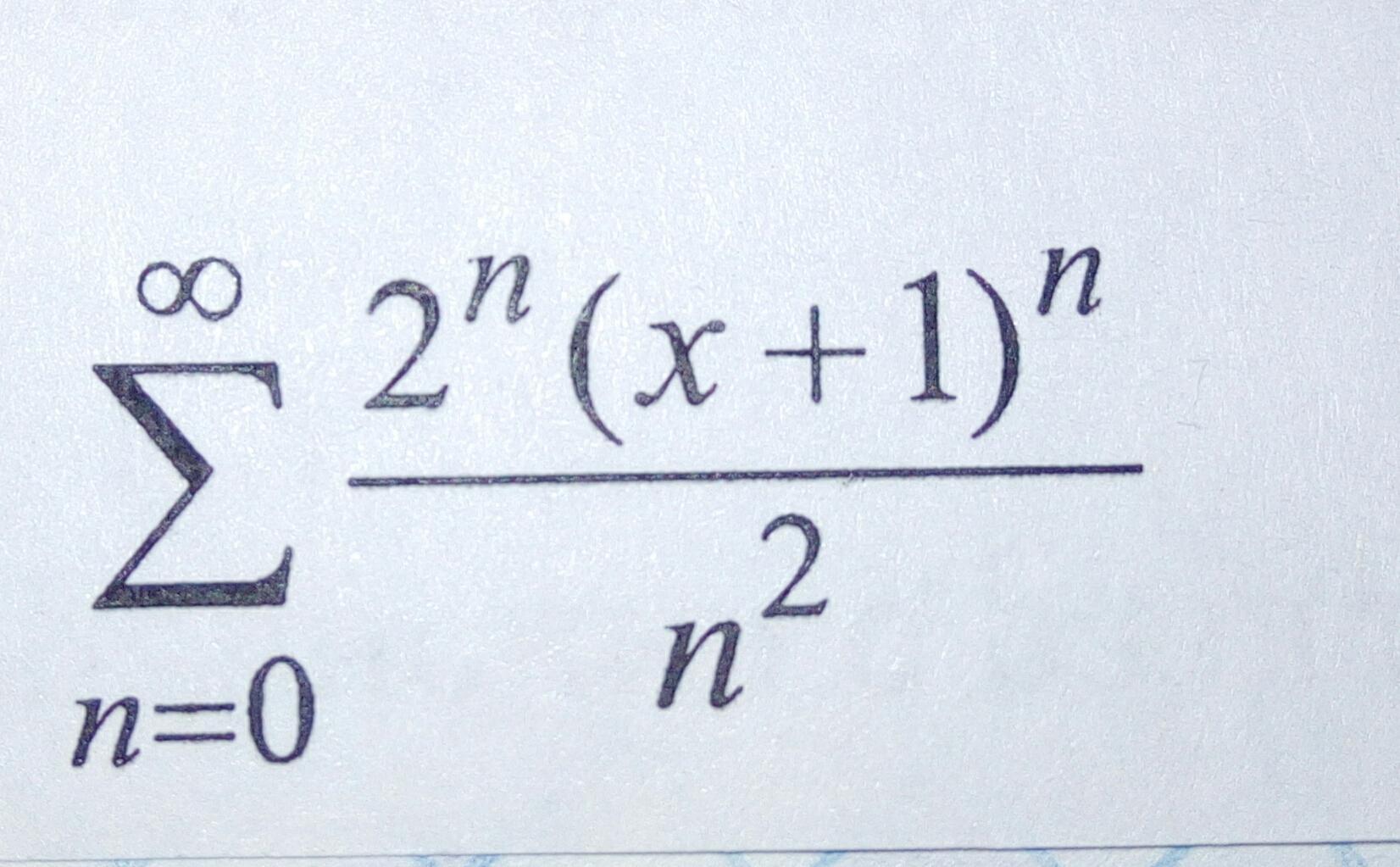
Ответы
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад