Помогите решить двойной интеграл!!!!!!!(очень срочно)
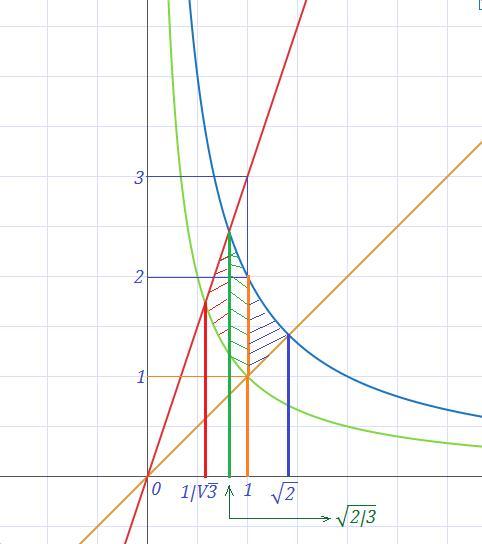
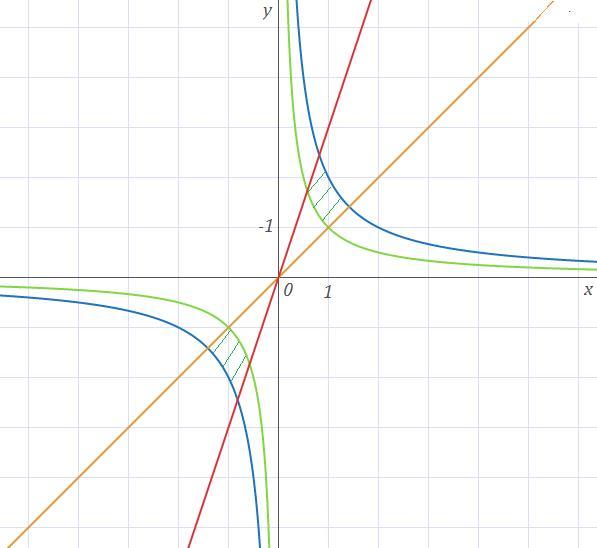
Первое задание:∫∫(x^2y^2+y^2)dxdy ,область D:{1/x≤y≤2/x;x≤y≤3x}
Ответы
Ответ дал:
0
Точки пересечения:
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад