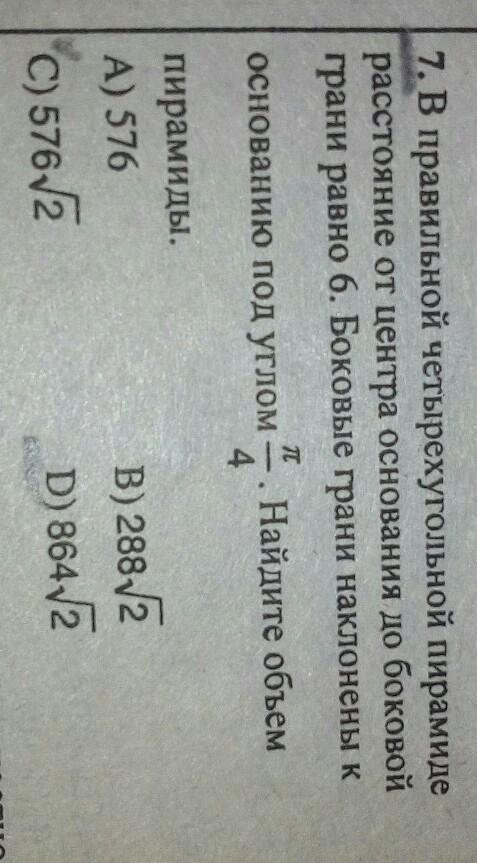Question

Геометрия. Срочно!!!​

Answer 1

π/4 = 45°

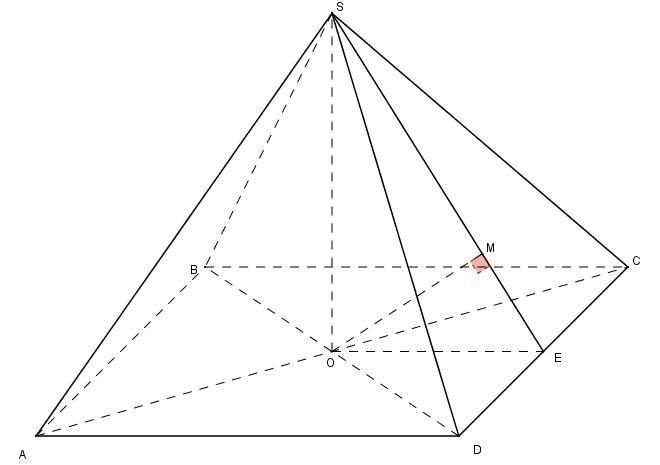
Расстоянием от центра основания до боковой грани является отрезок ОМ, перпендикулярный SE, по условию OM = 6; ∠SEO = 45°.

ΔEOM — прямоугольный равнобедренный; OE = OM√2 = 6√2. Также ΔSOE — равнобедренный прямоугольный; SO=OE = 6√2.

OE — радиус вписанной окружности основания; AD=2*r = 2*6√2 = 12√2. Теперь вычислим объем пирамиды

$V=frac{1}{3}S_oh=frac{1}{3}cdot(12sqrt{2})^2cdot 6sqrt{2}=576sqrt{2}$ куб. ед.

Ответ: 576√2 куб. ед.