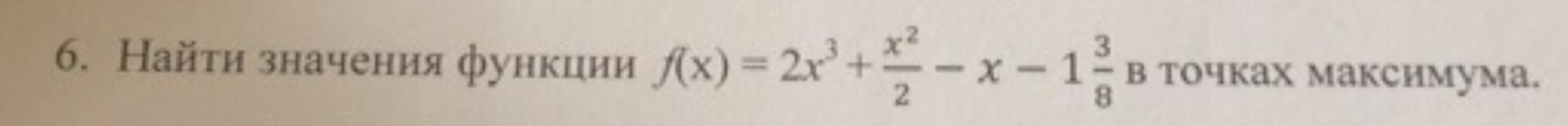Question

Решите 6 задание пожалуйста

Answer 1

Найдём производную и её нули:

$y'=6x^2+x-1\\6x^2+x-1=0\6(x-frac13)(x+frac12)=0\x_1=frac13\x_2=-frac12$

Определим знаки производной на интервалах:

$xin(-infty;;-frac12):; y'>0\xin(-frac12;;frac13):;y'<0\xin(frac13;;+infty):;y'>0$

В точке x = -1/2 производная меняет свой знак с положительного на отрицательный, значит, точка х = -1/2 - точка максимума.

$y(-frac12)=2cdotleft(-frac12right)^3+frac12cdotleft(-frac12right)^2-left(-frac12right)-1frac38=-frac14+frac18+frac12-frac{11}8=frac{14}8=1frac34$