Question

сколько корней имеет уравнение arcsinx=x??
с объяснением пожалуйста​

Answer 1

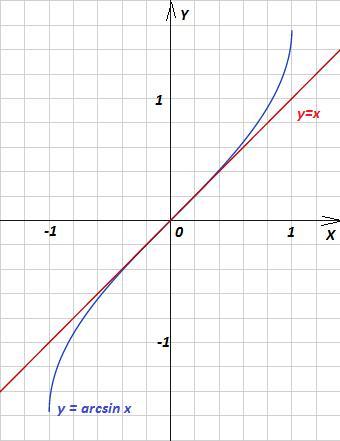
Рассмотрим две функции   g(x) = x   и   f(x) = arcsin x.

g(x) = x  -  линейная, строго монотонно возрастающая, нечётная непрерывная функция, D(g) = R. График - прямая линия, проходящая через начало координат.

f(x) = arcsin x   -  обратная тригонометрическая, строго монотонно возрастающая, нечётная непрерывная функция, D(f) = [-1; 1]. График - кривая линия, проходящая через начало координат.

Оба графика проходят через начало координат  (0;0).

$f'(x) = (arcsin~x)'=dfrac 1{sqrt{1-x^2}}neq 0;~~xneq pm1\\f''(x)=Big(dfrac 1{sqrt{1-x^2}}Big)'=dfrac x{(1-x^2)sqrt{1-x^2}}=0;~~x_0=0\\f'(0)=dfrac 1{sqrt{1-0^2}}=1$

Прямая  y=x  -   касательная к графику функции f(x) = arcsin x  в точке перегиба  x₀=0, то есть графики пересекаются только в этой точке.

Ответ : уравнение имеет единственный корень  x=0

Answer 2

Ответ:

Объяснение:    Решение :  ///////////////////////////

Answer 3

вместо " аналогично " : h( x ) - нечетная функция и значит , если нет корней на ( 0 ; 1 ) , то нет корней и на (-1 ; 0 ) ( если
f ( x ) = 0 при х от -1 до 0 , то f(-x) = - f(x) = 0 , причем -х от 0 до 1

Answer 4

небольшое уточнение : в первом и во втором случае ноль надо включить ( 0=

Answer 5

0=<х <1 и -1 < x < = 0

Answer 6

Уважаемые коллеги , не удаляйте пожалуйста комменты , они по делу