Question

Найти гипотенузу равнобедренного прямоугольного треугольника, если расстояние от середины катета до гипотенузы равно 3 см.

Answer 1

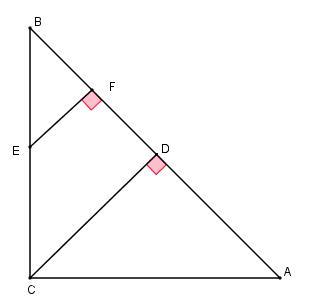
Поскольку прямоугольный треугольник равнобедренный, то у него катеты равны, т.е. BC = AC и ∠B = ∠A = 45°.

EF — расстояние от середины катета до гипотенузы. Тогда ΔBEF — равнобедренный прямоугольный треугольник, EF = BF = 3 см.

BE = EF√2 = 3√2 ⇒ BC = 2*BE = 6√2 см.

Из ΔABC:  гипотенуза AB = BC√2 = 6√2 · √2 = 12 см

Ответ: 12 см.

Answer 2

почему треугольник ВЕF равнобедренный?

Answer 3

Угол B = 45 и этот треугольник прямоугольный

Answer 4

Значит и угол BEF = 45

Answer 5

все понятно, спасибо!!!

Answer 6

свой ответ редактировать не буду, его надо удалить. Т.к. эту задачу я поняла после вашего решения и объяснения. А редактировать свой отает - это значит переписать ваше решение. Я считаю это нечестно и не солидно.

Answer 7

Ответ 12 см. Используем свойство средней линии треугольника, свойство равнобедренного треугольника и свойство медианы прямоугольного треугольника.