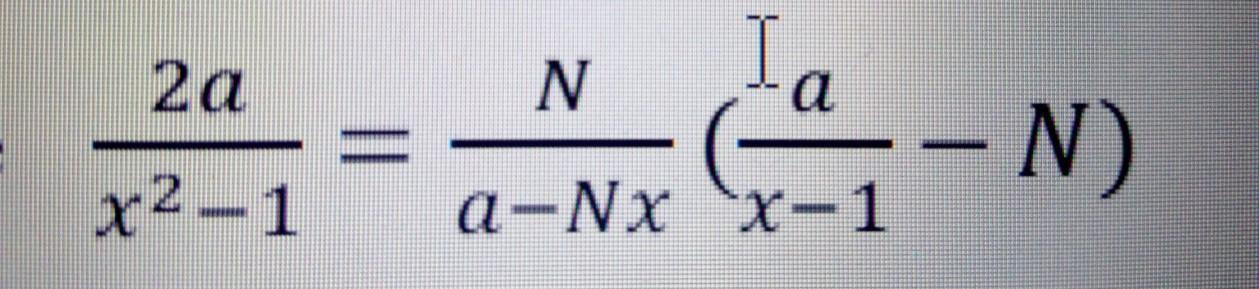Question

Помогите решить уравнение!!!
Даю 50 баллов
Где N=17

Answer 1

Ответ:

Объяснение:

2a/(x^2 - 1) = 17/(a - 17x)*(a - 17x + 17)/(x - 1)

ОДЗ x ≠ 1; x ≠ - 1; x ≠ a/17

Умножаем все на общий знаменатель (a-17x)(x-1)(x+1)

2a(a - 17x) = 17(x+1)(a+17-17x)

2a^2 - 34ax = 17(ax+a+17x+17-17x^2-17x)

2a^2 - 34ax = - 289x^2 + 17ax + 17a + 289

289x^2 - 51ax + (2a^2 - 17a - 289) = 0

Обычное квадратное уравнение с параметром.

D = 51^2*a^2 - 4*289(2a^2 - 17a - 289) = 289*(9a^2 - 8a^2 + 68a + 1156) =

= 289*(a^2 + 68a + 1156) = [17*(a+34)]^2

Так как D есть точный квадрат, то он неотрицателен при любом а.

При а = - 34 будет D = 0 и

x = 51a/(2*289) = - 3*17*2*17/(2*17^2) = - 3

При всех других а будет

x1 = [51a - 17(a+34)]/(2*289) = [3a - (a+34)] /34

x2 = [3a + (a+34)]/34